Lecture4

单变量的情况

优化问题通常是寻找使函数$f(x)$取得最小值的$x$。高中的时候我们就学过求极值的问题，解题的思路一般分为两步：1）先通过一阶导数为0求得函数的转折点。2）然后计算转折点的二阶导数来判断是极小值点还是极大值点（有可能是转折点）。整个的计算过程如图所示：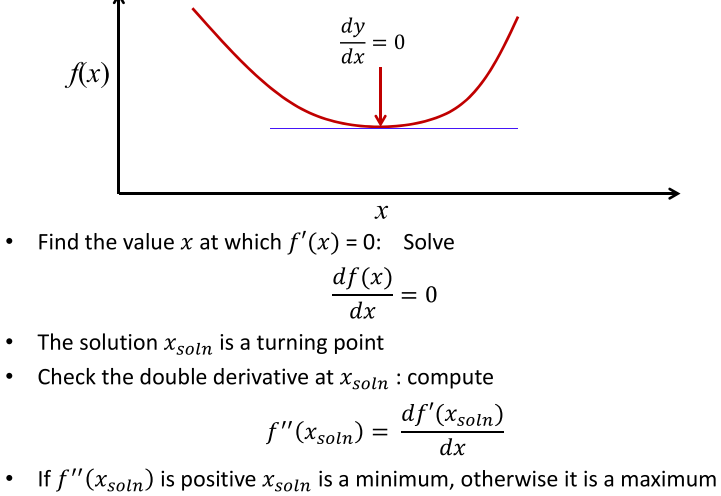

在单变量的函数中一阶导数为0的点通常有三种情况：极小值点，极大值点和拐点。为了得到函数的极小值通过二阶导数来进行判断，二阶导数的取值可以分为3种情况：

1) $\frac{d^2f(x)}{dx^2} \gt0$ 为极小值点

2) $\frac{d^2f(x)}{dx^2} \lt0$ 为极大值点

3) $\frac{d^2f(x)}{dx^2} =0$ 为拐点

三种情况如图所示

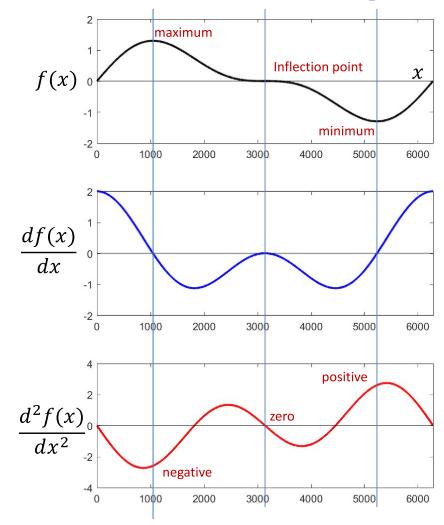
上述所讨论的情况都是针对于单变量的，当函数变为多变量的时候问题会变的稍微有点复杂，多变的情况也是神经网络所优化的形式。

多变量的情况

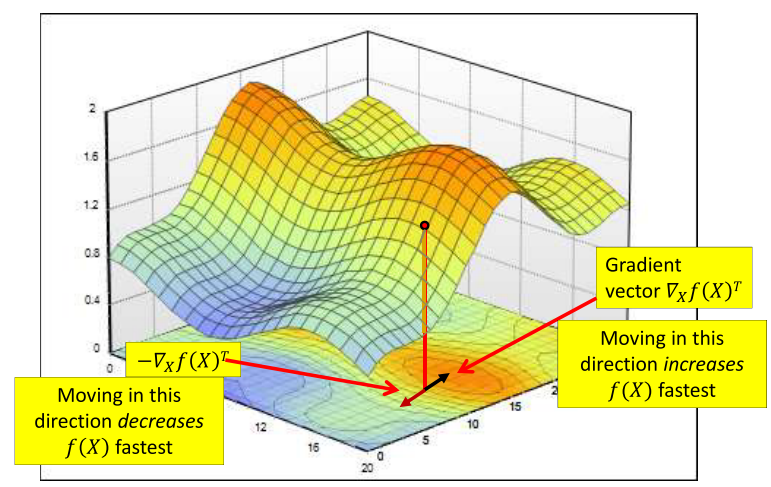
对于多变量函数的优化问题同样是寻找函数的转折点。在开始之前先引入多变量函数的”一阶导数”和”二阶导数”。对于多变量函数来说一阶导数的转置是函数的梯度，梯度的方向是函数增长最快的方向，如图所示：

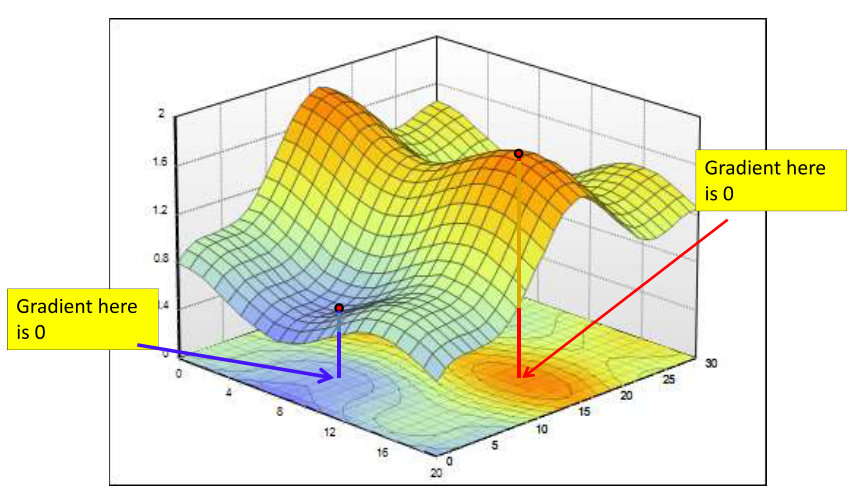
梯度为0的点有可能是函数的极大值点、极小值点或者鞍点，梯度为0的点如图所示：

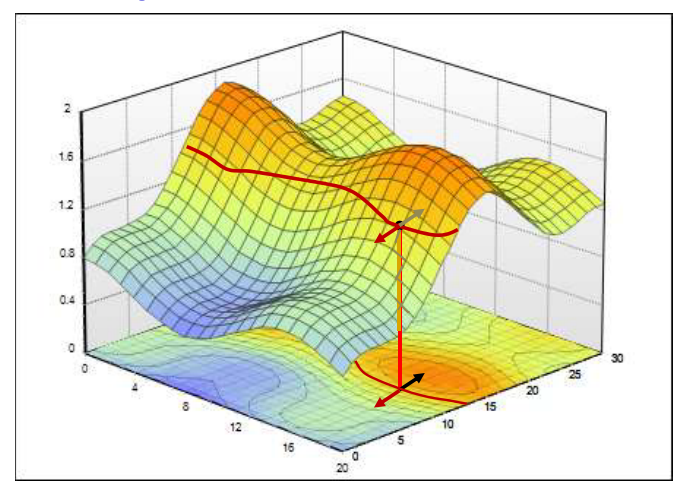
同时梯度的一个性质是垂直于登高线

上面所阐述的都是针对于一阶的情况，对于多变量函数进行二阶求导会得到一个Hessian矩阵。给定函数$f(x_1, x_2, x_3, …, x_n)$，则得到的二阶的导数如图所示

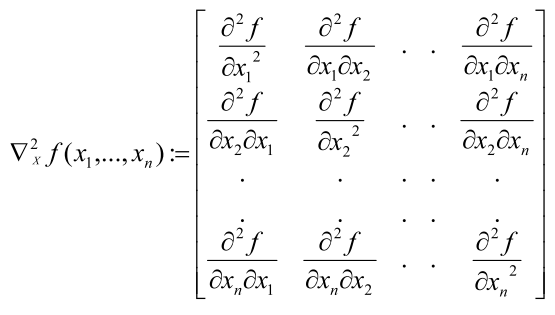
为了求得函数的极小值点，与单变量的求解过程相同，先求得使得一阶导数为0的点，既梯度为0的点，然后在这些梯度为0的候选点中计算其二阶梯度，Hessian矩阵然后判断。(函数无约束的情况下)

1) 求得使得梯度$\nabla_Xf(X)=0$的点，这些点为候选点。
2) 计算这些候选点位置的二阶导数$\nabla_X^2f(X)$(Hessian矩阵)，根据Hessian矩阵的值来判断

1) 如果Hessian矩阵是正定的(所有的特征值都是正的)—>可以判断为局部极小值点。
2) 如果Hessian矩阵是负定的(所有的特征值都是负的)—>可以判断为局部极大值点。

但是上述的方法中存在的一个问题，$\nabla_Xf(X)=0$的解出并不是容易的，有可能存在很难解的形式。在这种情况下迭代的解决方式是有效的。开始于一个随机的解$X$，然后迭代的调整直到最后获得正确的解。

迭代的求解最优解

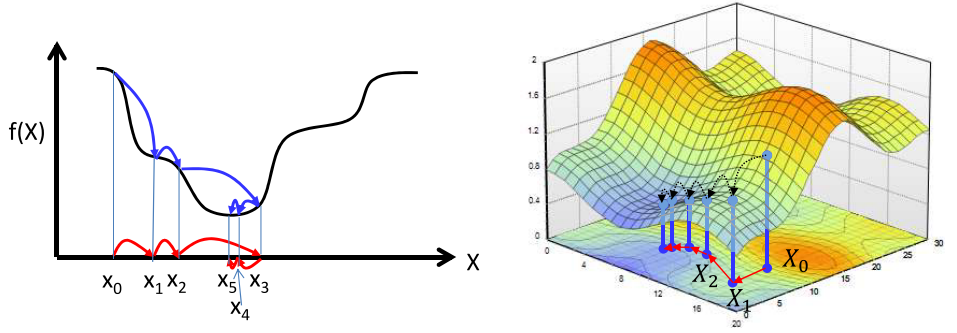
迭代的解决方式分以下步骤:

1) 对于优化的变量$X$，随机一个初始的值$X_0$。(可以思考神经网络参数的初始化问题，初始化的好坏会影响模型的优化)
2) 更新$X$的值，使得$f(X)$的值变小。
(参数的更新方式，设计出了很多优化的算法)
3) 当$f(X)$的值不再变小的时候，停止更新。

上述的叙述中细心的话会发现两个问题：

1) 更新的方向是哪里，我们怎样更新$X$的值让它从$X_0$得到最后的最优解。
2) 在每一步的更新中我们的步长是多少，大一点还是小一点。

对于更新的方向，如下图所示：

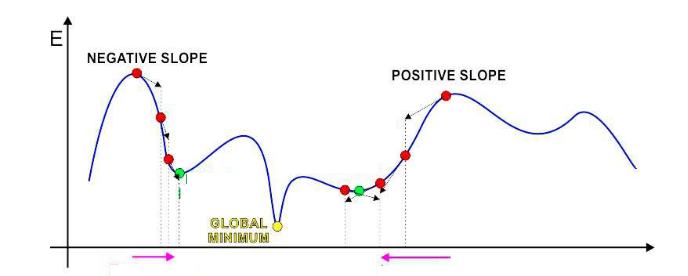
对于导数为正的，如果我们向左边更新$X$的值可以使得函数值减小。对于导数为负的，如果我们向右边更新$X$的值可以使得函数减小。所以总结出的更新方向为：

1) A positive derivative -> moving left decreases error
2) A negative derivative -> moving right decreases error

对于上述的过程用伪代码表示出来就可以得到一个平凡的梯度下降的算法：

1) Initialize $x^0$
2) while$f^{‘}(x^k)\neq0$
if $sign(f^{‘}(x^k))$ is positive:
     $x^{k+1} = x^k-step$
else:
    $x^{k+1} = x^k+step$

通过观察后面的if else 语句可以合并成一句
$x^{k+1}=x^k-sign(f^{‘}(x^k))step$

所以可以改写为

1) Initialize $x^0$
2) while$f^{‘}(x^k)\neq0$
$x^{k+1}=x^k-\eta^kf^{‘}(x^k)$

其中的$\eta^k$是步长(step size)

综上我们可以通过梯度下降或者梯度上升的方式来迭代的求得函数的最小值或者函数的最大值。

1) 为了求得极大值点，沿着梯度的方向更新(梯度上升)。
$x^{k+1}=x^k+\eta^{k}\nabla_xf(x^k)^T$
2) 为了求得极小值点，沿着梯度的反方向更新(梯度下降)。
$x^{k+1}=x^k-\eta^{k}\nabla_xf(x^k)^T$

(从数学上的角度来看，梯度的方向是函数增长速度最快的方向，那么梯度的反方向就是函数减少最快的方向)

剩下最后一个问题什么情况下，函数收敛，停止更新。

1) $|f(x^{k+1}-f(x^k))|<\epsilon_1$
2) $||\nabla_xf(x^k)||<\epsilon_2$

上述两者是或者的关系。如图所示：

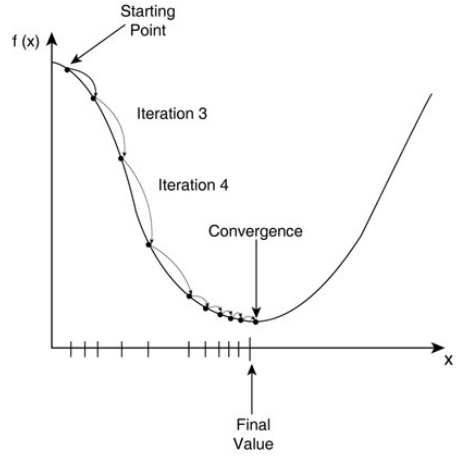
所以整个的梯度下降的算法可以用如下的伪代码表示:

1) Initialize:
$x^0$
$k=0$
2) do

1) $x^(k+1)=x^k-\eta^k\nabla_xf(x^k)^T$
2) $k=k+1$
3) while $|f(x^(k+1)-f(x^k))|>\epsilon$

通过梯度下降的方式求得函数的解有以下两种的情况：

1. 对于凸的函数(convex)，通过梯度下降的方式总能找到函数的最小值得点。

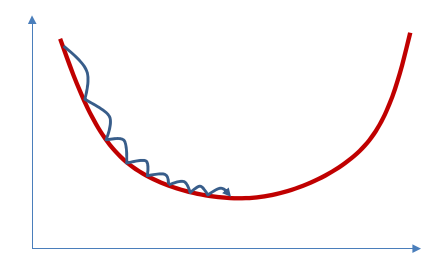
2. 对于非凸的函数(convex)，通过梯度下降的方式找的点可能是局部极小值的点也可能是鞍点(图中是拐点)。在神经网络中，我们绝大部分遇到的是这种情况。

What is f()? Typical network

Typical network

激活函数

下文讲述了两种激活函数，一种是作用于多个输入产生一个输出，另一种也作用于多个输入但是输出也为多个(Vector Activations)。

1) 在神经网络中，一般情况下每个神经元作用于一个输入的集合产生一个输出，如图所示

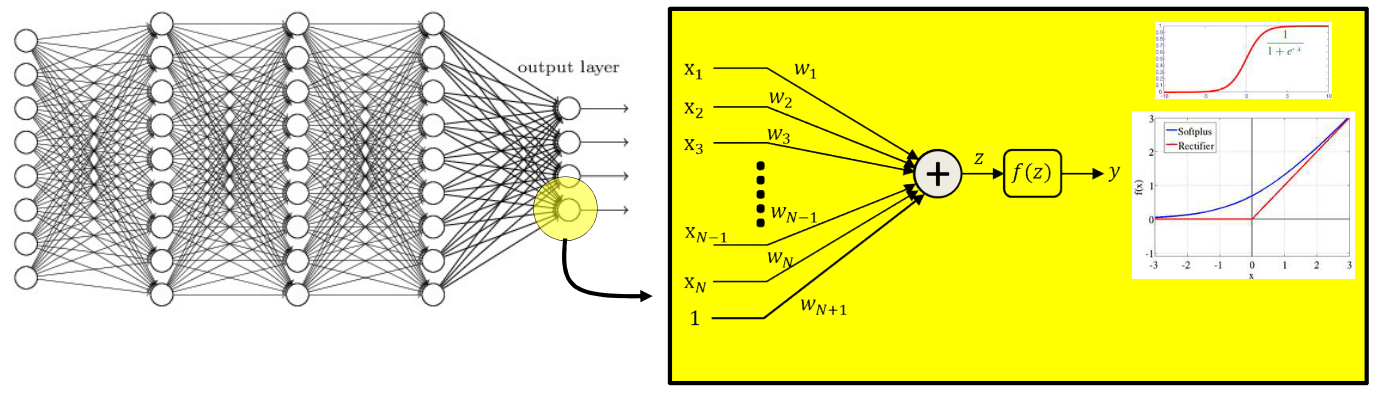
其中神经元的一般表达式为：
$y=f(\sum_iw_ix_i+b)$

对于激活函数来说，更加一般的设置为任何可导的函数都可以作为激活函数
$y=f(x_1,x_2,…x_N;W)$
其中神经元的参数为权重$w_i$和偏置$b$

2) 上述的激活函数有一个共同的性质，都是对输入的线性组合然后激活产生一个标量的结果，神经网络中也存在一种激活产生多个输出，其表达式为：
$[y_1,y_2,…,y_l]=f(x_1,x_2,…,x_k;W)$
函数$f()$作用于一系列的输入产生一些列的输出，对于任何一个权重$W$的修改都会影响全部的输出。这种类型的激活函数课上老师命名为”Vector Activations”

下面讲述一个向量激活的例子(Softmax)

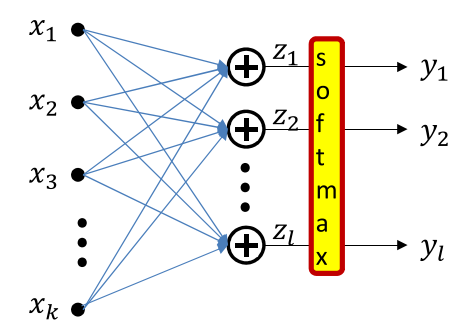
整个过程的表达式为
$$z_i=\sum_jW_{ji}x_j+b_i$$
$$y=\frac{\exp(z_i)}{\sum_j\exp(z_j)}$$

激活函数本身没有参数，这边的参数同多输入单输出的激活函数是相同的。
在分层的神经网络中，每一层的感知机可以看成是一个向量激活函数。

What are these input-output pairs?

下面讲述第二个问题输入输出的表示，神经网络的输入输出有多种形式，例如以下几种形式
vector of pixel values
vector of speech features
real-valued vector representing text
other real valued vectors

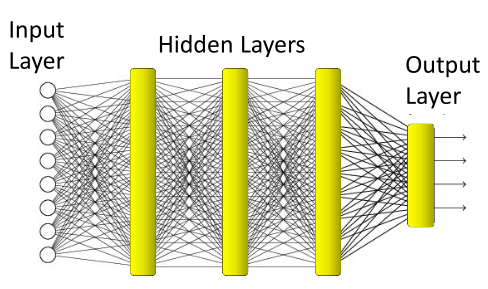
对于神经网络的输出，输出可能是单个的标量，也有可能是向量。

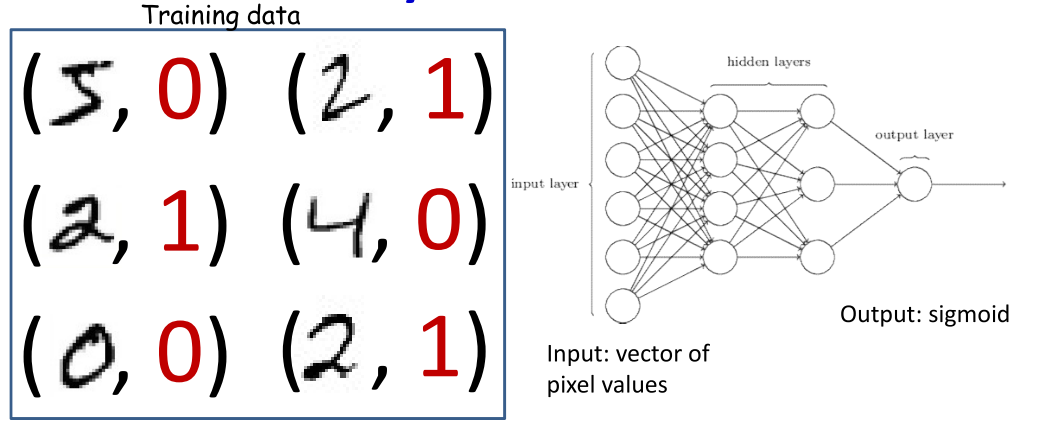
1) 当输出为标量时，例如输出是二分类的(is this a cat or not)时候，我们通常用$1/0$来代表期望的函数输出
1=Yes it’s a cat
0=No it’s not a cat
在这种情况下，输出的激活函数通常为Sigmoid，激活函数的输出解释为类别为1的条件概率$P(Y=1|X)$值。
2) 除了上述的表示外，网络的输出有可能是两个，其中一个代表期望的输出，另外一个代表期望输出的负类，在这种情况下输出变成了2-output softmax

1. yes: –>[0, 1]
2. no: –>[1, 0]

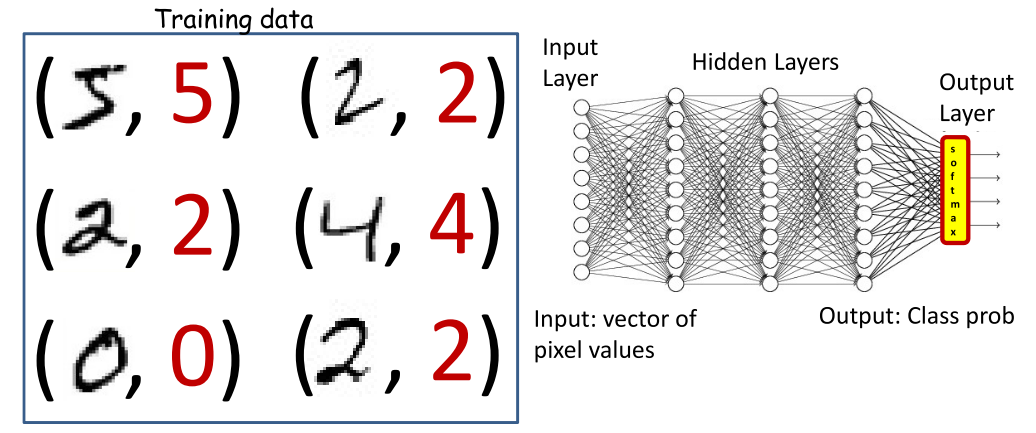
对于多分类的输出通常用one-hot的形式表示，这边就不详细解释了。对于多类别的情况，最后输出层的激活函数通常用softmax来表示
$$z_i=\sum_jw_{ji}^{(n)}y_j^{(n-1)}$$
$$y_i=\frac{\exp(z_i)}{\sum_j\exp(z_j)}$$
$y_i$可以看做为类别$i$的条件概率值$y_i=p(class=i|X)$

下面通过一个例子来解释清楚神经网络的输入和输出。对于下面的手写数字的数据集，分两个任务

1) Binary recognition: Is this a “2” or not
2) Multi-class recognition: Which digit is this? Is this a digit in the first place?

1. Binary classification

   

2. Multiclass classification

   

学习神经网络的参数使其做期望的工作。

What is the divergence div()?

通过对上述三个问题的描述1)神经网络的构造，2)输入输出的定义(数据集)，3)损失函数的定义。已经可以搭建基本的神经网络了，剩下的问题就是对神经网络的优化过程。可以回顾一下开始的问题定义:
1). 给定训练数据集的输入输出对$(X_1,d_1), (X_2,d_2),(X_3,d_3),…(X_T,d_T)$
2). 计算在第i个实例上的损失$div(Y_i,d_i)$，其中$Y_i=f(X_i;W)$
3). 计算整体的损失为
$$Loss=\frac{1}{T}\sum_idiv(Y_i,d_i)$$
4). 最小化损失来优化权重{${w_{ij}^{(k)},b_j^{(k)}}$}

网络的训练是通过梯度下降的方式来实现的，这些已经在开头讲过，梯度下降的伪代码可以用如下的方式来表示:

1. Initialize all weights{$w_{ij}^{(k)}$}
2. Do:
   1. For all i, j, k, initialize $\frac{dLoss}{dw_{i,j}^{(k)}}=0$
   2. For all t=1: T:
      – Compute $\frac{dDiv(Y_t,d_t)}{dw_{i,j}}$
      –$\frac{dLoss}{dw_{i,j}^{(k)}}+=\frac{dDiv(Y_t,d_t)}{dw_{i,j}^{(k)}}$
   3. For every layer $k$ for all i,j:
      $$w_{i,j}^{(k)}=w_{i,j}^{(k)}-\frac{\eta}{T}\frac{dLoss}{dw_{i,j}^{(k)}}$$
3. untill $\color{red}{\text{Err}}$ has converged

所以现在剩下的问题就是求解$\frac{dDiv(Y_t, d_t)}{dw_{i,j}^{(k)}}$