Multi-layer Perceptrons as universal Boolean functions
- MLPs are universal Boolean functions
- Any function over any number of inputs and any number of outputs
- But how many “layers” will they need?
在多层感知机表达布尔表达式的时候多少层是适合的。
如下面的真值表,真值表就是一个布尔表达式。
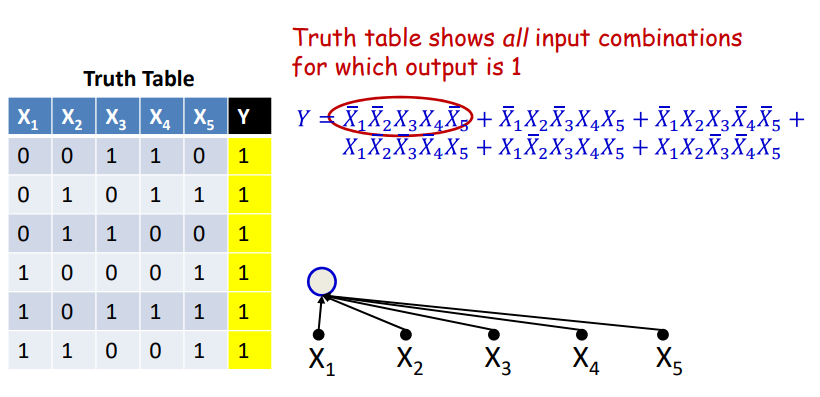
上图中的真值表是使用合取范式的形式表示的还没有化简,用多层感知机来对上述的表达式进行表示。如图表达式中第一项可以表示为各个项的AND操作,如图中的第一个神经元。后续的操作可以增加相应的神经元。如下图所示
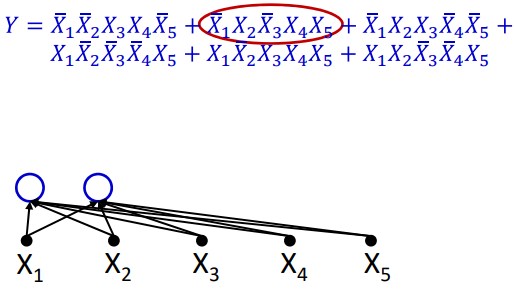 |
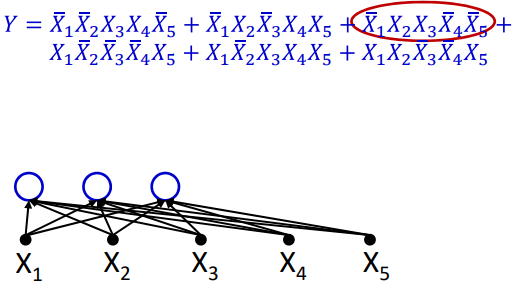 |
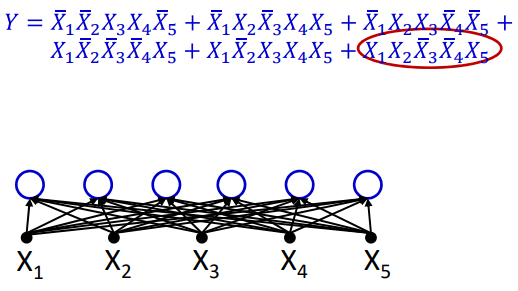 |
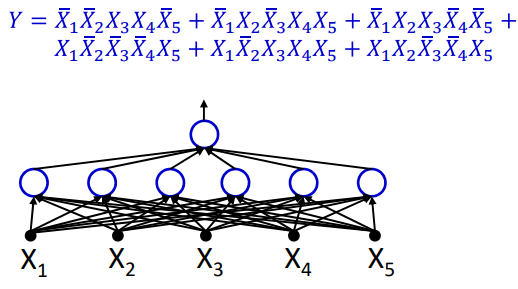 |
通过上述的表示得到如下的结论:
- 任何的真值表都可以用这种方式来表示
- A $\color{red}{one-hidden-layer}$ MLP is a Universal Boolean Function
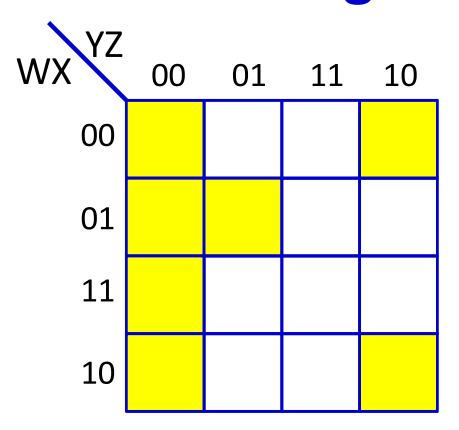
如上的卡诺图所示,每个黄色的区域为1,白色的区域为0,则没有化简之前的表达式为
$Y = \overline{WXYZ}+\overline{WX}Y\overline{Z}+\overline{W}X\overline{YZ}+\overline{W}X\overline{Y}Z+WX\overline{YZ}+W \overline{X}YZ+W\overline{X}Y\overline{X}$
如果像第一个例子那样来构造感知机模型需要7项表达式。
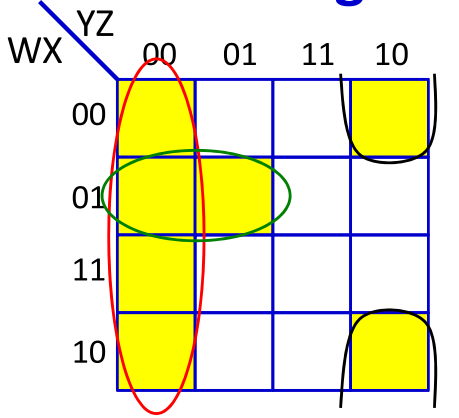
如图对其进行化简可以得到的表达式为
$Y = \overline{YZ}+\overline{W}X\overline{Y}+\overline{X}Y\overline{Z}$
则这样只需要3个神经元就可以完成。通过对上述的析取范式进行化简得到了更加简单的网络。
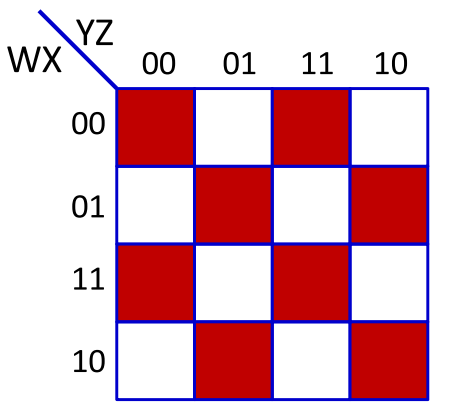
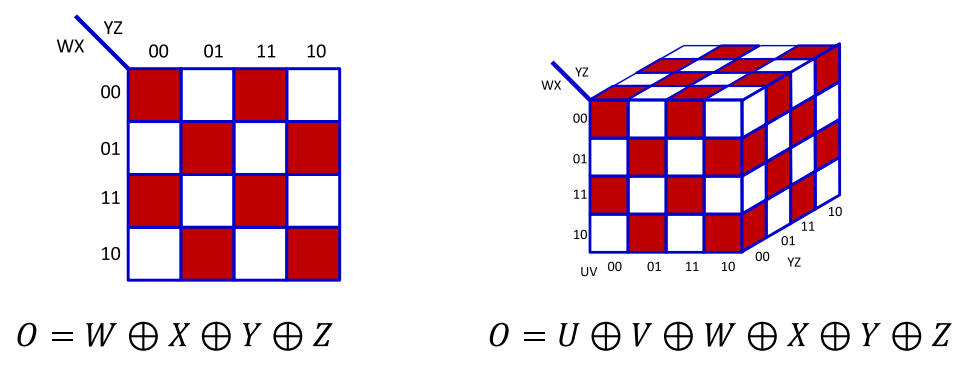
但是当表达式不能化简的时候,如图得到了一个最大的不能化简的表达式。这样如果用一个隐藏层的表达式来表示则需要8个神经元。
当增加两个变量的时候如图所示,用单层表示的时候需要32个神经元。
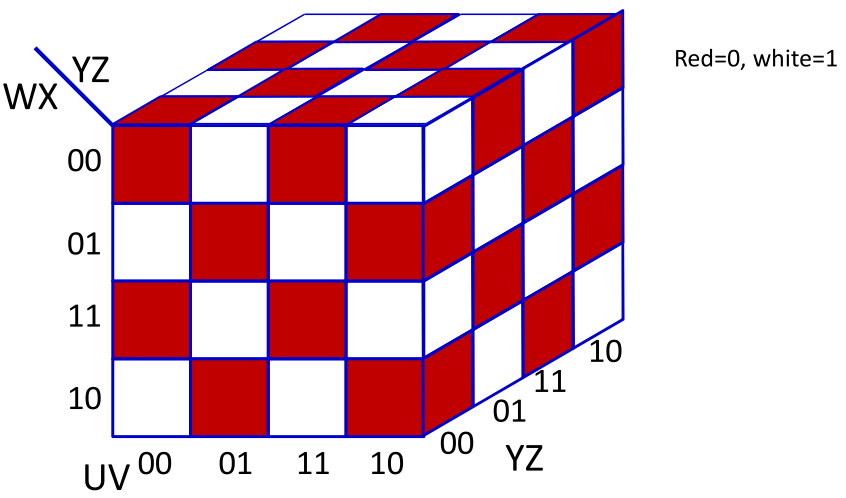
由此可以推广到当有N个变量,用单层的感知机来表示,最大的需要$2^{N-1}$个隐层的单元。
如果我们用多层感知机的时候,需要多少个神经元。
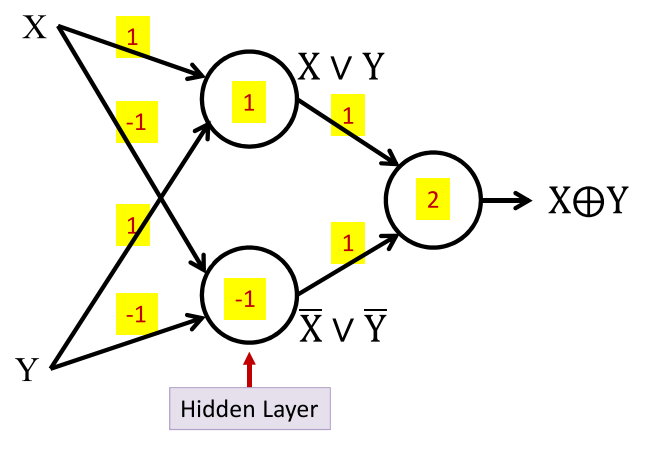
如图所示是使用异或表达式来表示的,异或在上一届中已经讲述过,异或表达式需要3个感知机单元来表示。
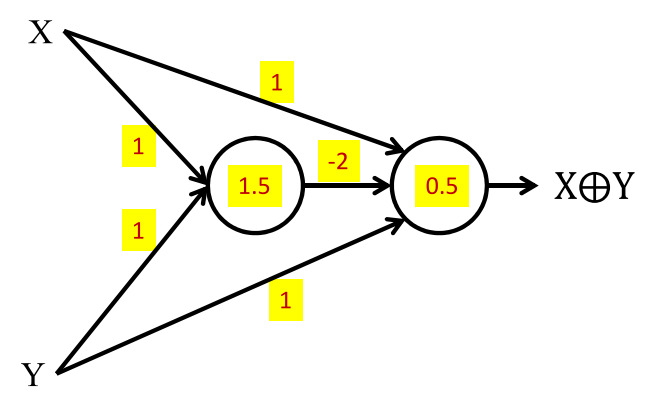
可以对其进行进一步的化简,如图所示两个神经元就可以表示。
当用第一种异或的方式来表示4个变量的最大表达式,如图则需要9个感知机。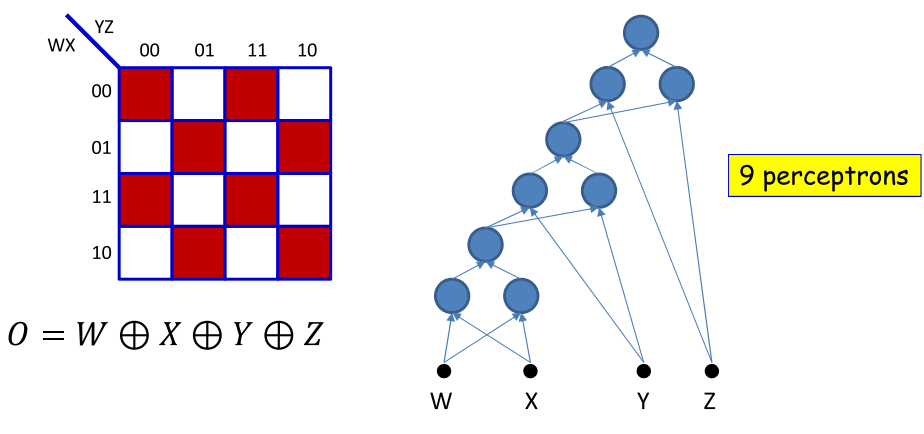
同理当表示6个变量的时候如图需要15个单元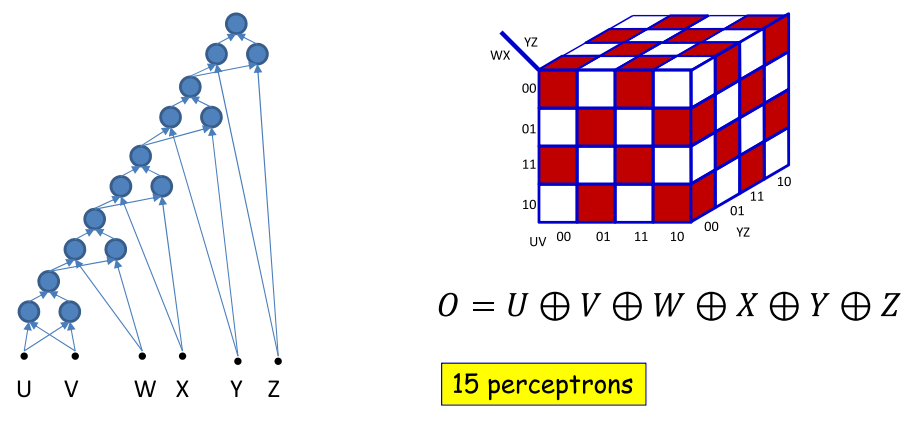
因此可以总结出,如果多层则需要的单元格式是$3(N-1)$
综上可以得到如下的结论:
- Single hidden layer: Will require $2^{N-1}+1$ perceptrons in all (including output unit)Exponential in N
- Will require $3(N-1)$ perceptrons in a deep network (Linear in N!!!)
当用如下的方式表示的时候,需要更少的神经元。
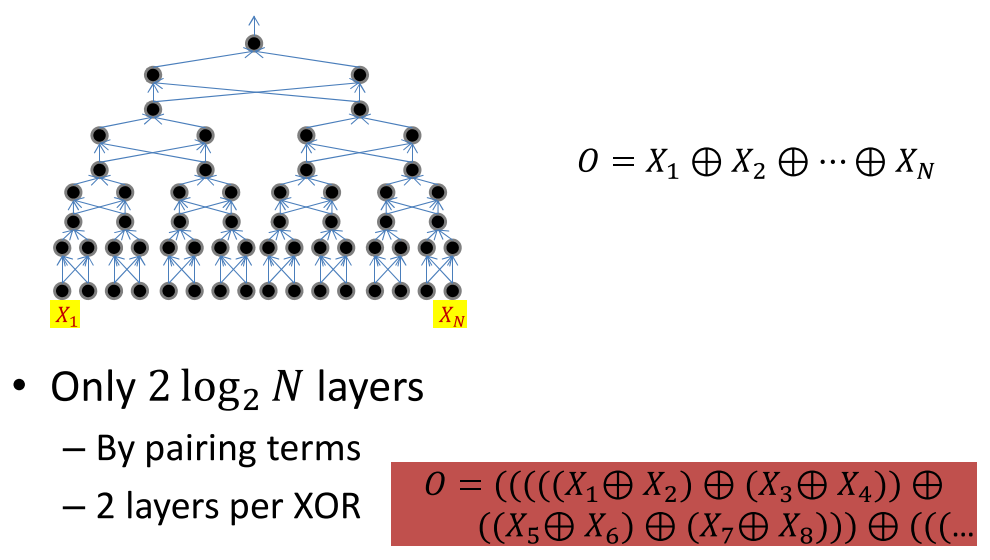
the challenge of depth
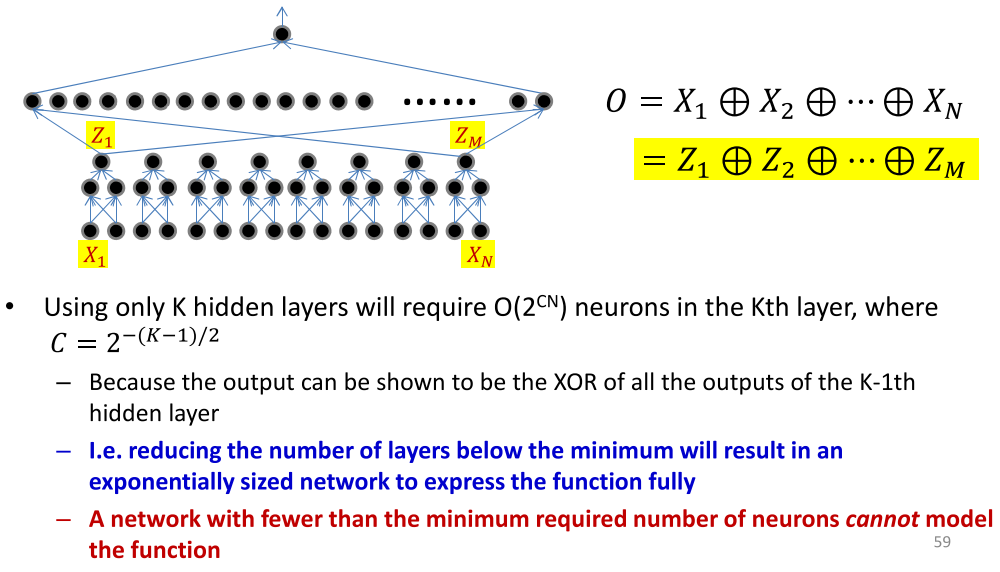
当只用k个隐层来表示的时候需要$O(2^{CN})$的神经元在第k层,在这边的$C=2^{-(K-1)/2}$,所以第k层有$CN$的神经元。
减少层数,将导致神经元指数级的上涨。如果小于最小的神经元的个数将不能来表示模型。
The actual number of parameters in a network
在神经网络中真正的参数,是各个神经元之间的连接的个数,神经元的个数在构建模型的时候是很重要的,对于有指数级别的神经元则需要指数级别的权重,甚至更多,所以用深层的网络可以有效的减少权重的个数。
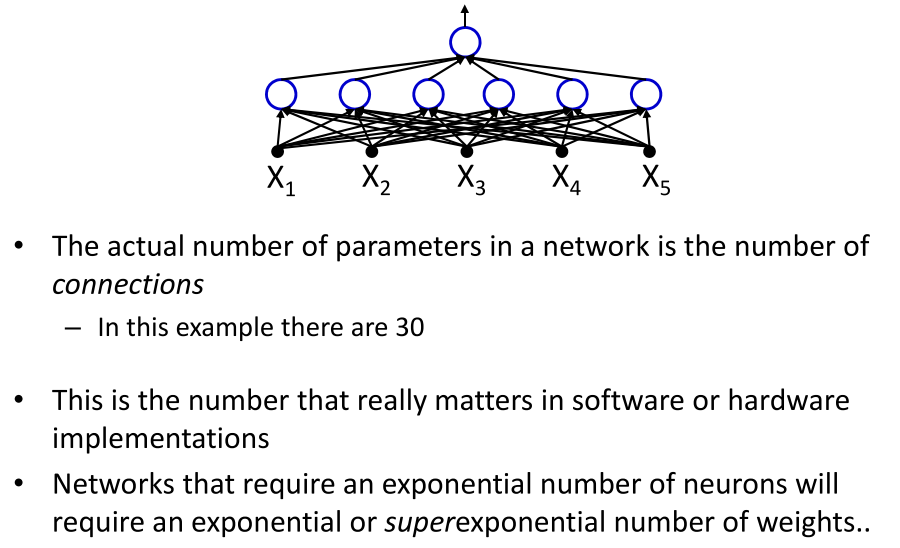
The need for depth
- Deep Boolean MLPs that scale linearly with the number of inputs …
- … can become exponentially large if recast using only one layer
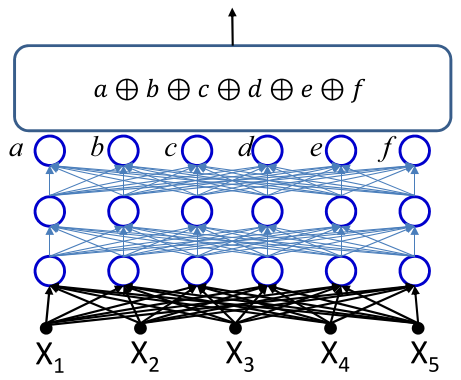
- The wide function can happen at any layer
- Having a few extra layers can greatly reduce network size
summary
- An MLP is a universal Boolean function
- But can represent a given function only if
- It is sufficiently wide
- It is sufficiently deep
- Depth can be traded off for (sometimes) exponential growth of the width of the network
- Optimal width and depth depend on the number of variables and the complexity of the Boolean function
- Complexity: minimal number of terms in DNF formula to represent it
Story so far
- Multi-layer perceptrons are Universal Boolean Machines
- Even a network with a single hidden layer is a universal Boolean machine
- But a single-layer network may require an exponentially large number of perceptrons
- Deeper networks may require far fewer neurons than shallower networks to express the same function
- Could be exponentially smaller
MLPs as universal classifiers
由上一节可以知道,多层感知机可以构建复杂的决策边界,如图所示。
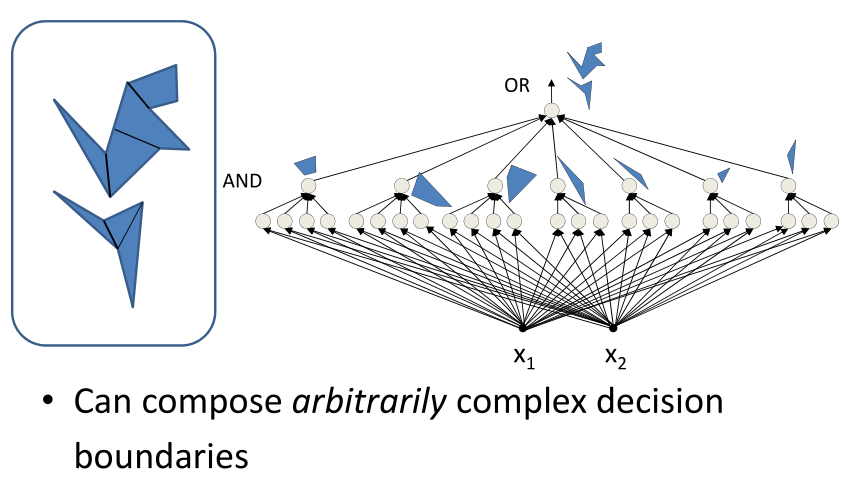
如果只用一层隐藏层,怎么来表示上面的结果。下面的图为上一节课中的例子,怎样用右边的一个隐藏层的感知机来表示。
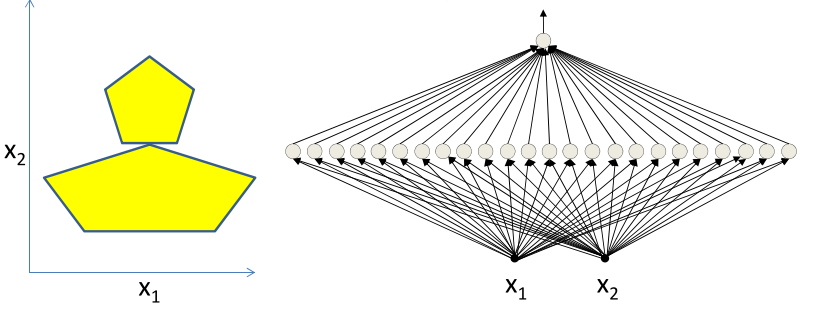
先进行一系列的推导
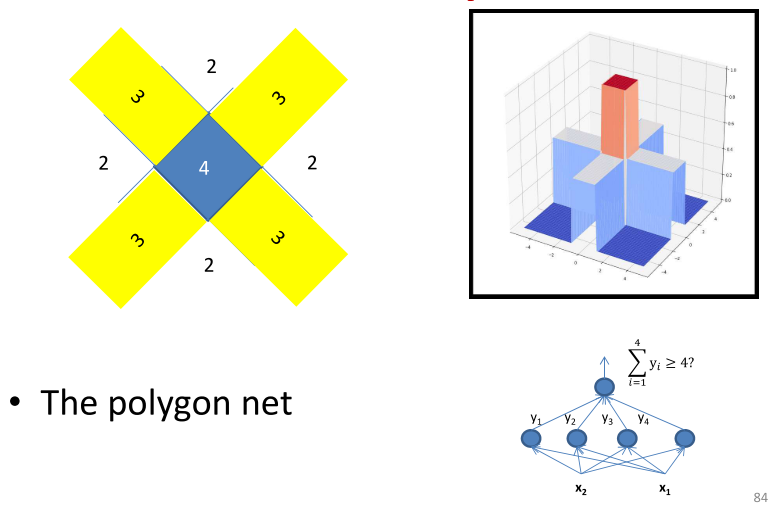
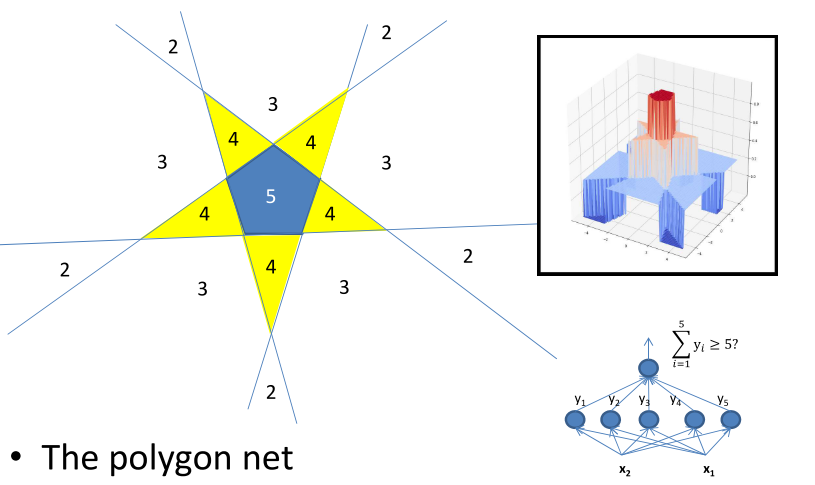
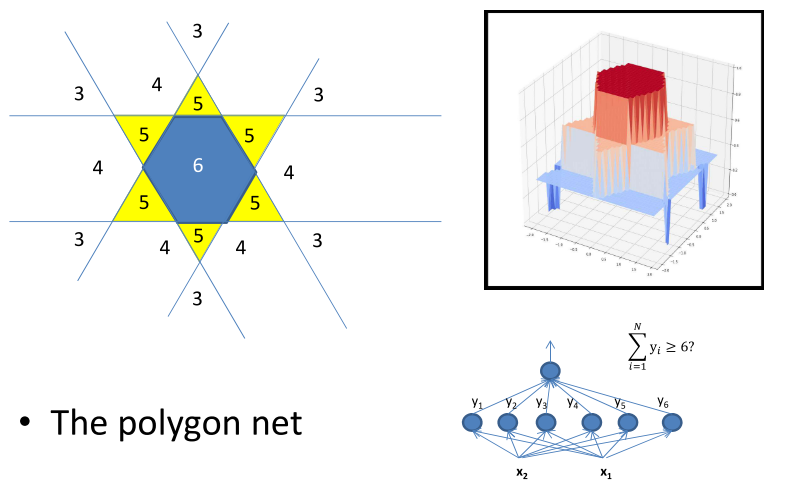
经过上面的一系列的递推,可以推导一下在用感知机组成的不同区域值为多少。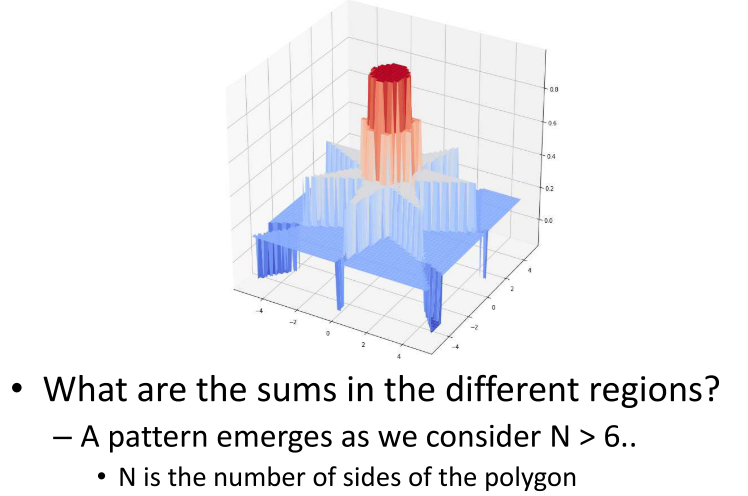
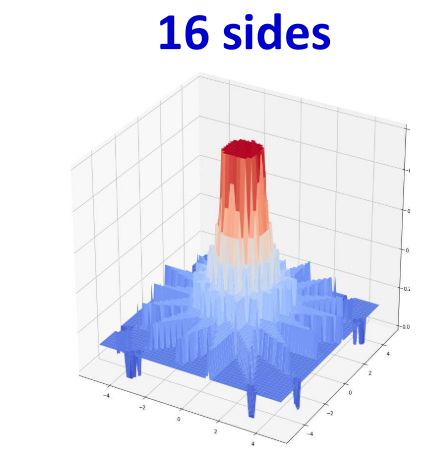
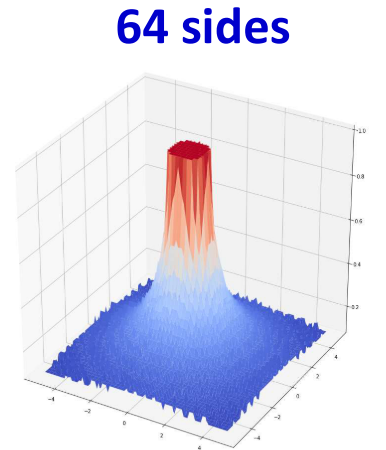
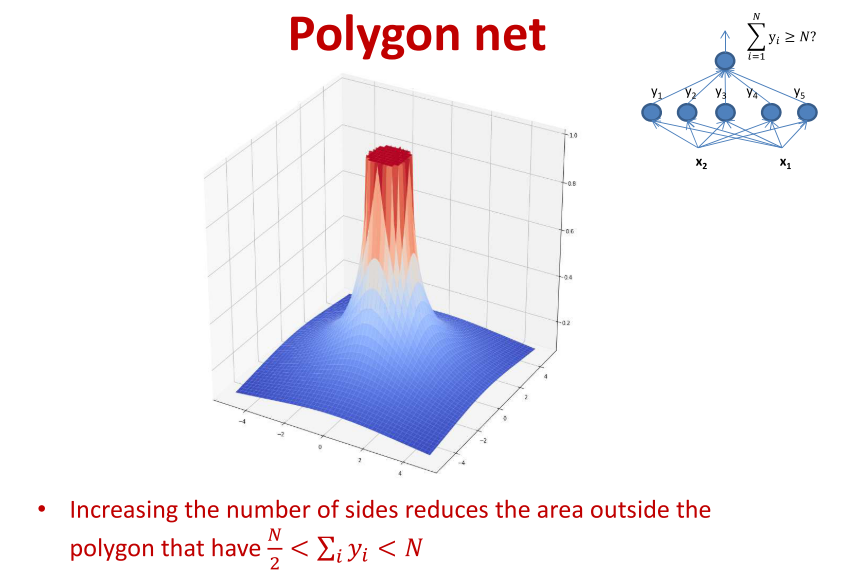
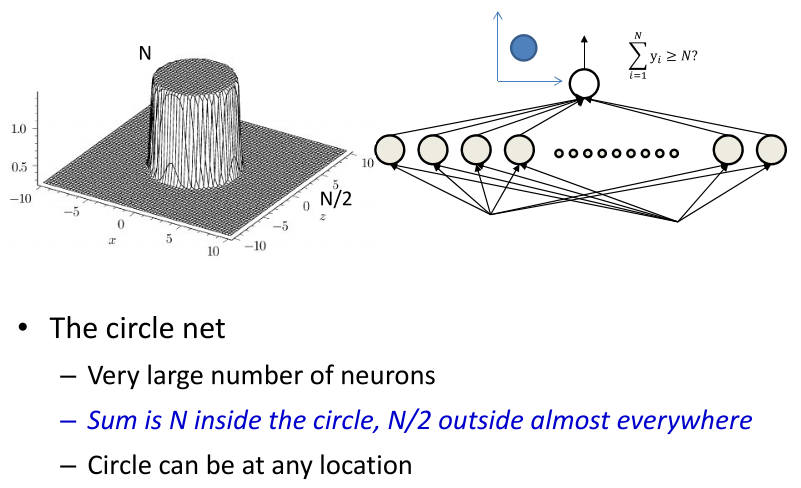
当N到达极限的时候,可以组成如下的图形,其中中间的值为N,边缘位置为N/2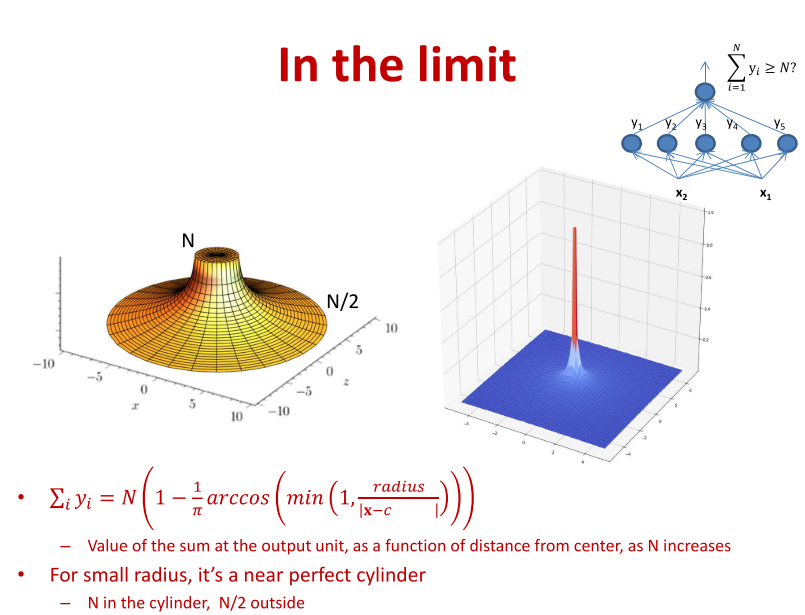
经过上面一系列的推导与结论,可以用上述的方式组成一个圆柱,通过非常多的神经元来实现,其中在圆柱体内部的值为N,在圆柱体外其他的地方几乎都为N/2,而且圆柱的位置可以是任意的。
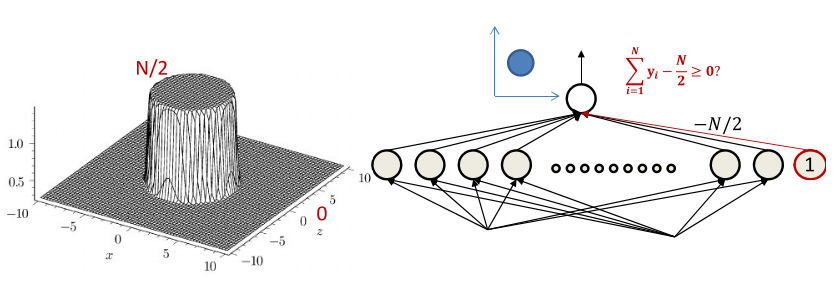
当整体减去一个偏置项就可以让圆柱外面的值为0,如图所示。
同时可以将不同的圆柱体组合在一起来构建复杂的图形,如图所示。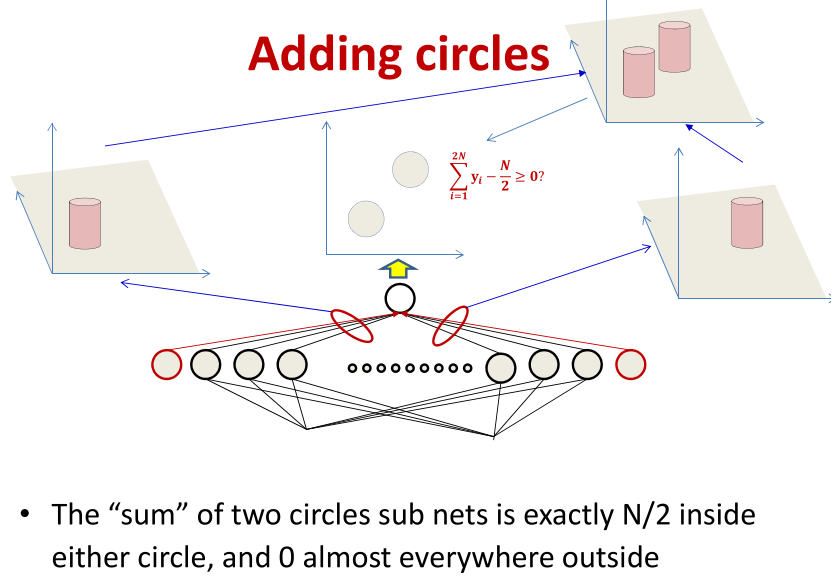
Composing an arbitrary figure
通过上面的结论,来组成任意的图形。
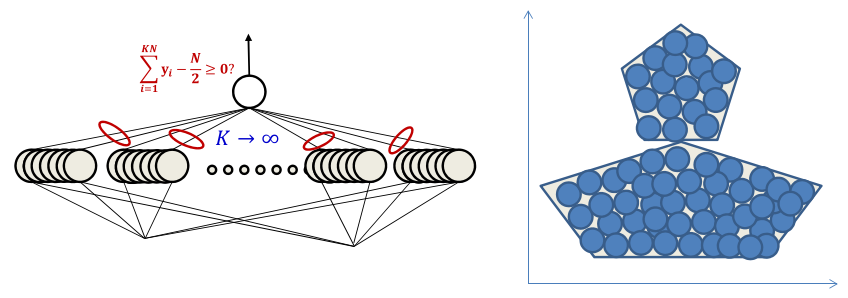
- Just fit in an arbitrary number of circles
- More accurate approximation with greater number of smaller circles
- Can achieve arbitrary precision
- MLPs can capture any classification boundary
- A one-layer MLP can model any classification boundary
- MLPs are universal classifiers

- Deeper networks can require far fewer neurons
Optimal depth
下面列举一个复杂的例子