“BIBO” Stability
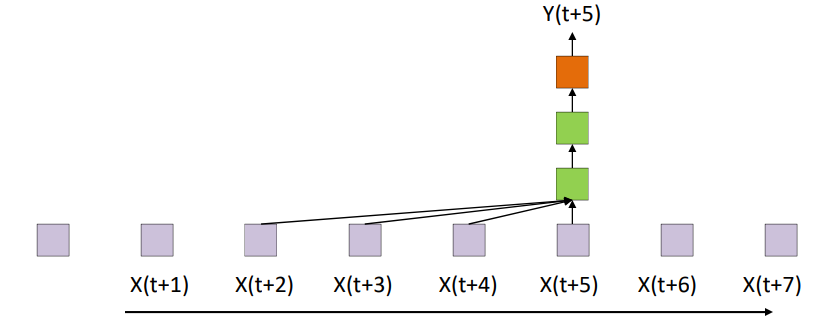
- Time-delay structures have bounded output if
- The function $f()$ has bounded output for bounded input(which is true of almost every activation function)
- $X(t)$ is bounded
- “Bounded Input Bounded Output” stability
This is a highly desirable characteristic
下面的部分来分析RNN是否具有”BIBO”的性质,为了便于分析,课程中先是用线性的激活函数来分析后面进行推广。
Linear systems
- Easier to analyze linear systems
- Will attempt to extrapolate to non-linear systems subsequently
- All activations are identity functions
所以在以下的分析中
$$z_k=W_{h}h_{k-1}+W_{x}x_{k}$$ $$h_{k}=z_{k}$$
解:综合上面两个等式可以得到
$h_k=W_{h}h_{k-1}+W_{x}x_{k}$
$h_{k-1}=W_{h}h_{k-2}+W_{x}x_{k-1}$
将第二个等式带入第一个得
$h_k=W_h^2h_{k-2}+W_hW_{x}x_{k-1}+W_{x}x_{k}$
以此递推下去可以得到
$h_k=W_{h}^{k+1}h_{-1}+W_{h}^{k}W_{x}x_{0}+W_{h}^{k-1}W_{x}x_{1}+W_{h}^{k-2}W_{x}x_{2}+…+W_{h}^{2}W_{x}x_{k-2}+W_{h}W_{x}x_{k-1}+W_{x}x_{k}$
注:$W_{h}^kW_{x}x_0$对应着在$t=0$时刻输入为$x_0$的项,其它的项全为0,其它的项类似,这边引入了一个新的函数$H_{k}(x_i)$,例如:
$H_{k}(x_0)=h_{k}(h_{-1}=0, x_0=x_0, x_1=0, x_2=0,…)$相当于只有$x_{0}$处有值,其它位置为0。
则上述等式等价为:
$h_{k}=H_k(h_{-1})+H_k(x_0)+H_k(x_1)+H_k(x_2)+…$
针对其中的一项$H_k(x_0)=W_{h}^kW_xx_0=x_0(W_h^kW_x1_0))=x_0H_k(1_0)$
其中$H_k(1_t)$是在时刻t的输入对最后输出$h_{k}$的影响。其中输入为[0 0 0 0…1 0 0]在t时刻的输入为1其它时刻为0,同时$h_1$也可以按相同的方式处理。所以最终可以等价于
$h_{k}=h_{-1}H_k(1_{-1})+x_0H_k(1_0)+x_1H_k(1_1)+x_2H_k(1_2)+…$
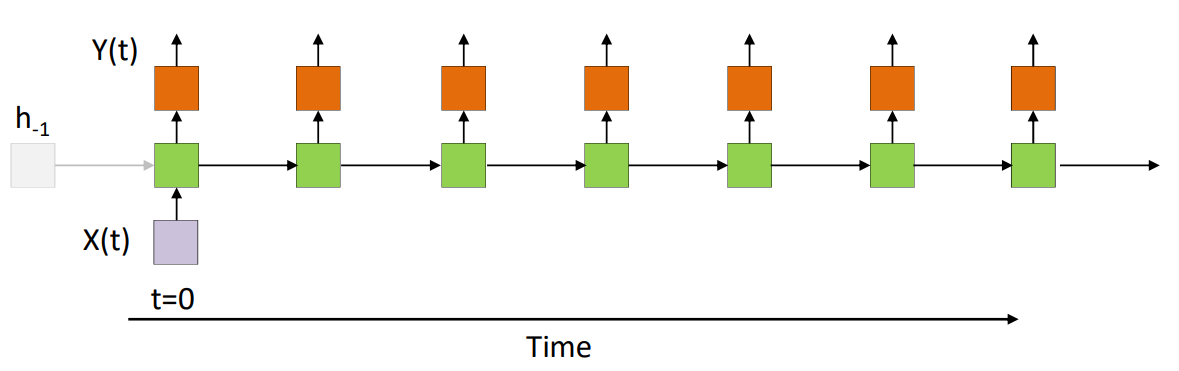
在RNN中主要是对之前信息的记忆,老师在课上原话是”How well does it remember at an input at time 0”所以我们这边重点分析在$t=0$时刻的,因为其它时刻是类似的都是$H_k(1_x)$的形式(感觉上述所有的推导都是为了推导出每个隐藏状态都是相同的形式,然后分析其中一项就可以)。课程中这边又用新的方式定义了上述的操作
$h(t)=wh(t-1)+cx(t)$这个等式与$h_k=W_{h}h_{k-1}+W_{x}x_{k}$是等价的只是更换了表示,则同时$H_k(x_0)=W_{h}^kW_xx_0$这一项等价与$h_0(t)=w^tcx(0)$就是h(t)的展开表示中在0时刻的项为h_0(t)这个也是最后h(t)对0时刻信息保留的多少。
所以综上这边得到两项为
- $h(t)=wh(t-1)+cx(t)$
- $h_0(t)=w^tcx(0)$ (Response to a single input at 0)
$h_0(t)$的值就代表着记忆的信息多少
如图所示横坐标为t,每条曲线对应着不同的w值,这边是针对t时刻的输入时标量的形式,可以发现当w的值大于1的时候,函数会很快的以指数的形式增长(blow up),当w小于1的时候,函数会值很快的下降(vanish),所以对信息的记忆很大程度上依赖于w的值。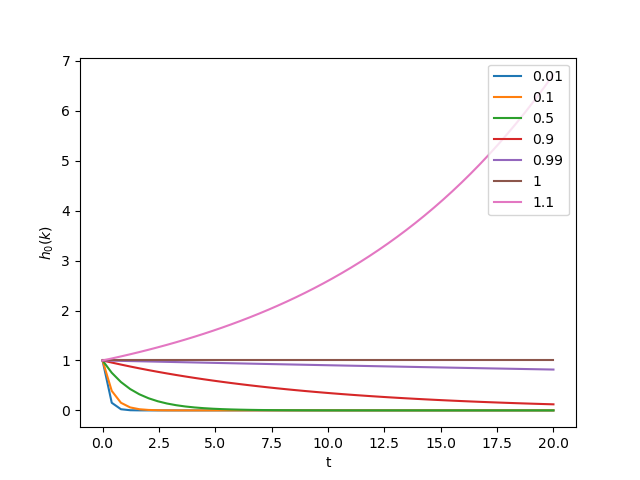
以上的分析是基于输入是标量形式的下面分析输入是向量形式的。
Linear recursions: Vector version
$$h(t)=wh(t-1)+cx(t)$$ $$h_0(t)=w^tcx(0)$$
解:$W$是矩阵,可以分解为$W=U \Lambda U^{-1}$,则根据线性代数矩阵特征值特征向量$Wu_i=\lambda_iu_i$,所以在W的特征向量所张成的空间中所有的向量都可以用特征向量的线性组合来表示,所以
这边假设$x’=Cx$则
$x’=a_1u_1+a_2u_2+…a_nu_n$
左右都乘以$W$得
$Wx’=a_1Wu_1+a_2Wu_2+…a_nWu_n$,
根据$Wu_i=\lambda_iu_i$化简得
$Wx’=a_1\lambda_1u_1+a_2\lambda_1u_2+…a_n\lambda_1u_n$
连乘$W$后得
$W^tx’=a_1\lambda_1^tu_1+a_2\lambda_1^tu_2+…a_n\lambda_1^tu_n$
$\displaystyle \lim_{x\to\infty}|W^tx’|=a_m\lambda_m^tu_m$
where $m=\underset {j}{argmax}\lambda_j$
综上课程中得到以下几个结论




课程中老师也分析了向量的形式得到了相同的结果。
How about non-linearities(scaler)
$$h(t)=f(wh(t-1)+cx(t))$$
下面分析当激活函数不是线性的时候,如图所示
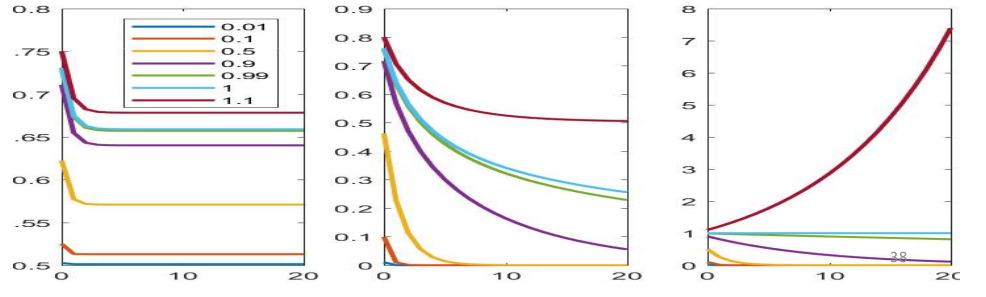
- sigmoid(left):不管初始化的w值为多少,很快的饱和。
- tanh(middle):对初始化的w比较敏感,可以保留一定时间的信息但是最终也会饱和。
- relu(right):对初始的w值比较敏感,可能below up。
下面这张图是当输入为负数的时候的结果图。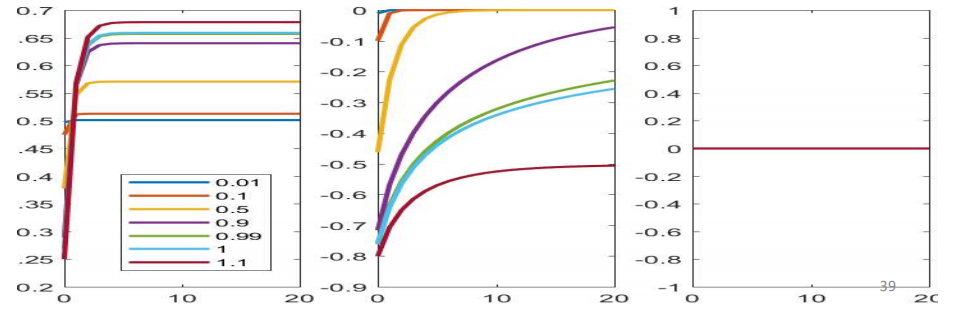
Stability Analysis
课程中老师后面讲解了当输入为向量的时候,得到了相同的结论,综上只有tanh函数可以满足能够在短时间内的记忆(only the tanh activation gives us any reasonable behavior and still has very short “memory”)

对于RNN网络的总结
• Excellent models for time-series analysis tasks
– Time-series prediction
– Time-series classification
– Sequence prediction..
– They can even simplify problems that are difficult for MLPs
• But the memory isn’t all that great.
总上RNN不能够长期的记忆信息,即使使用tahn激活函数也是在短时间内的记忆,不能够满足长期记忆的任务。
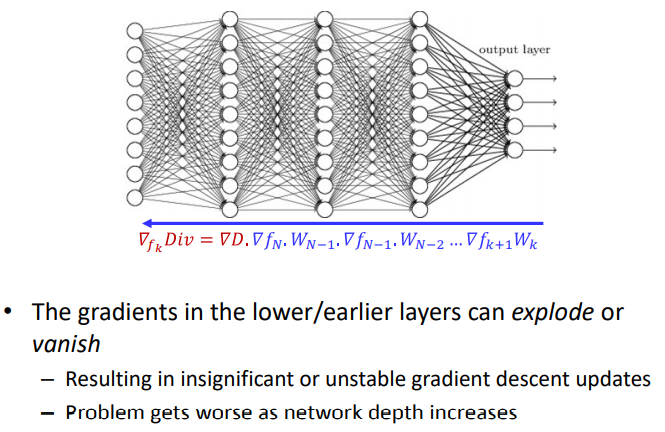
The Jacobian of the hidden layers for an RNN
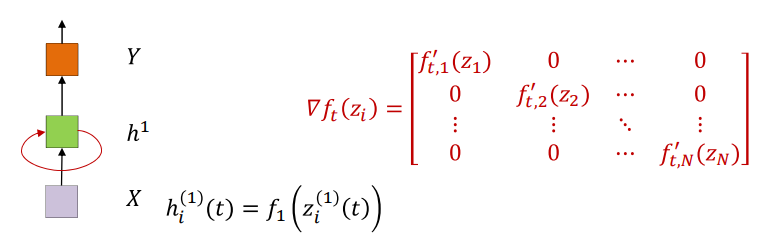
如图中的$\nabla f_t()$是隐藏层的输出对于隐藏层输入的梯度,只是对激活函数的求导
$$h(t)=f(wh(t-1)+cx(t))$$ $$z=wh(t-1)+c(x)$$
这边的h和z都是向量,所以求导是矩阵,但是每个输入只和一个输出有关系,所以是对角矩阵。对于激活函数例如$sigmoid(), tanh(), relu()$它们的梯度总是小于1的,对于RNN最常用的激活函数是$tanh()$,$tanh$的梯度是永远不会大于1的,如图
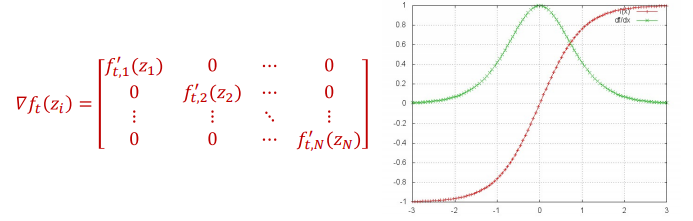
所以对于上面的对角矩阵是有界的,因为对角线上的每一项都是对$tanh$的求导。所以乘以上述的矩阵就会缩放。Multiplication by the Jacobian is always a shrinking operation.
对于
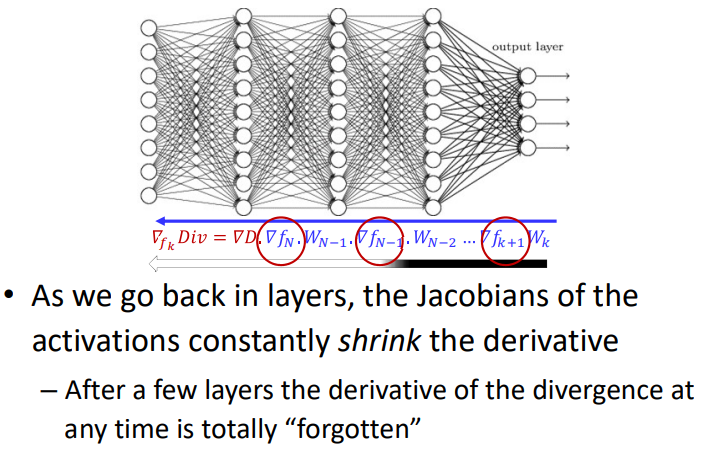
$Div(X)=D(f_N(W_{N-1}f_{N-1}(W_{N-2}f_{N-2}(…W_0X))))$
计算梯度得到
$\nabla_{f_k}Div=\nabla D·\nabla f_N·W_{N-1}·\nabla f_{N-1}·W_{N-2}…\nabla f_{k+1}W_k$
在上述的公式中当我们进行反向传播计算梯度的时候,当乘以Jacobian矩阵($\nabla f_N$)的时候,梯度就会shrink。在经过几层的方向传播,梯度就会被忘记。
Training deep networks
如图在训练神经网络的时候,随着梯度的反向传播,梯度有可能消失
What about the weights
在RNN中,所有的权重的矩阵都是相同的

Exploding/Vanishing gradients

Gradient problems in deep networks
在神经网络的前向传播中浅层的梯度可能消失或者爆炸,可能会造成不明显的或者不稳定的梯度的更新,而且会随着网络层的加深,问题变得严重。
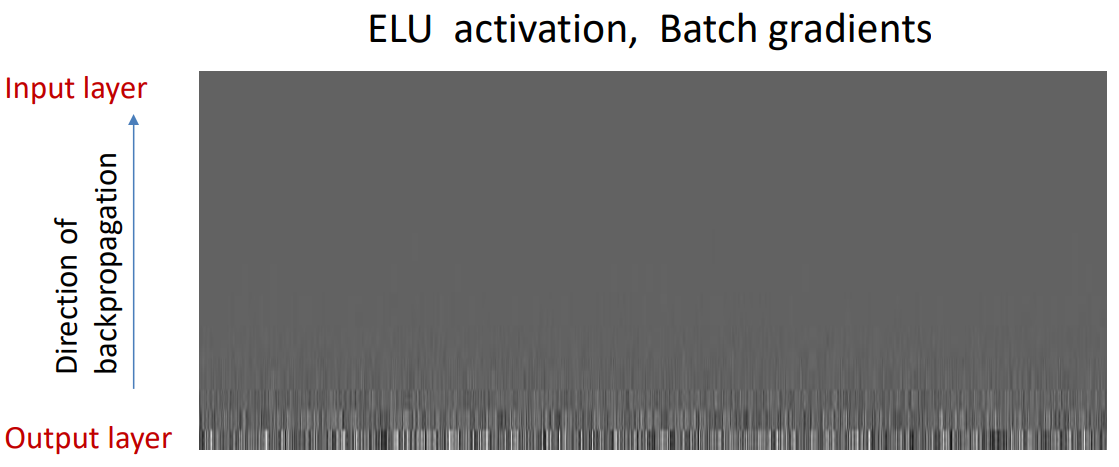
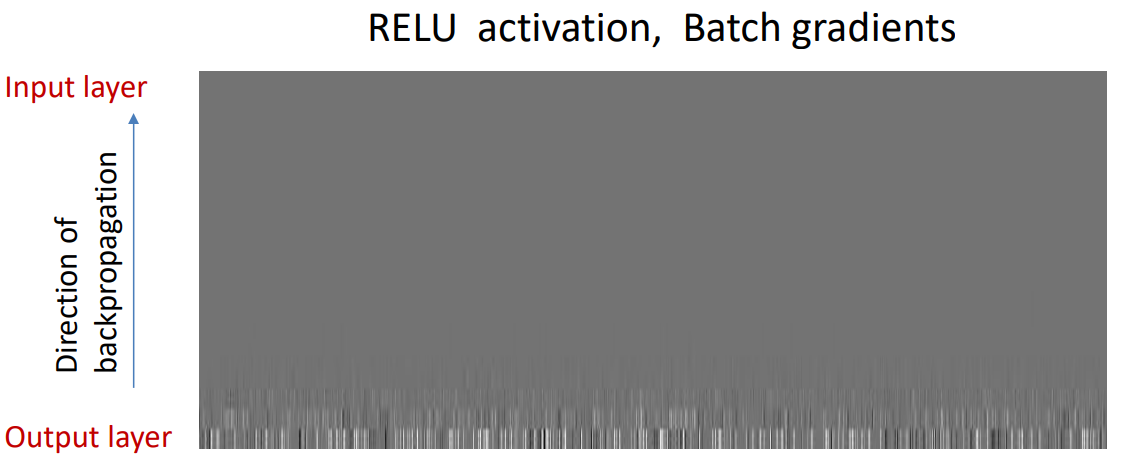
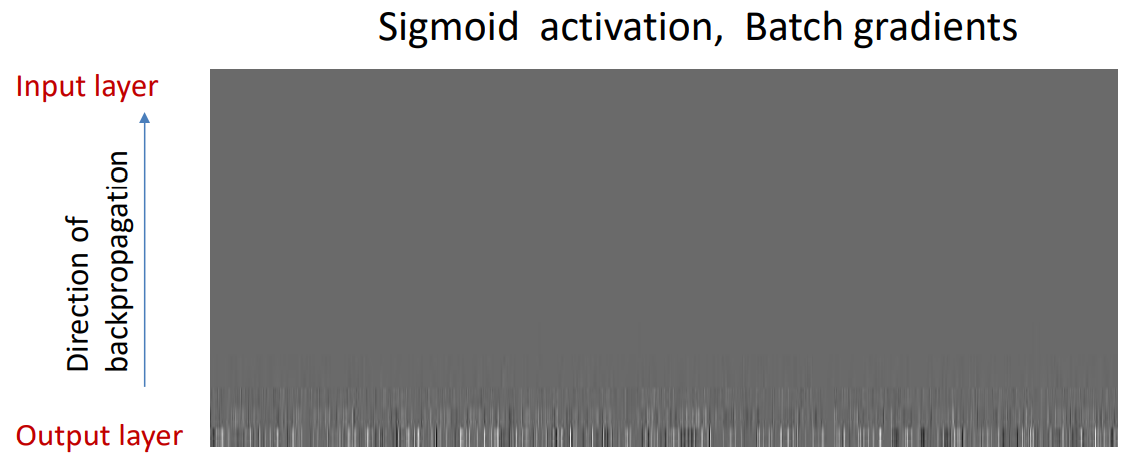
后面老师对比了不同激活函数的梯度消失
 |
 |
 |
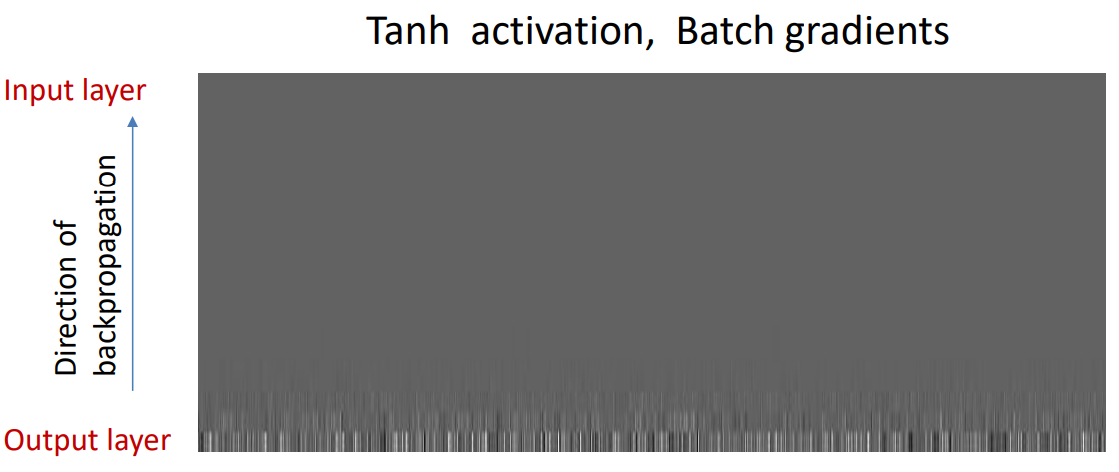 |

story so far
通过以上的实验,老师从前向传播中rnn对之前信息的记忆和在反向传播过程中梯度对网络更新两个方面进行了分析。得出了一下的结论。
- Recurrent networks retain information from the infinite past in principle
- In practice, they are poor at memorization
- The hidden outputs can blow up, or shrink to zero depending on the Eigen values of the recurrent weights matrix
- The memory is also a function of the activation of the hidden units (Tanh activations are the most effective at retaining memory, but even they don’t hold it very long)
- Deep networks also suffer from a “vanishing or exploding gradient” problem
- The gradient of the error at the output gets concentrated into a small
number of parameters in the earlier layers, and goes to zero for others
- The gradient of the error at the output gets concentrated into a small
从以上的分析,针对RNN中存在着的这些问题,下面讲解LSTM。先将上面存在的两个问题再具体的描述一下。
1、梯度在反向传播的过程中会消失

2、在前向传播的过程中,前面的信息会被忘记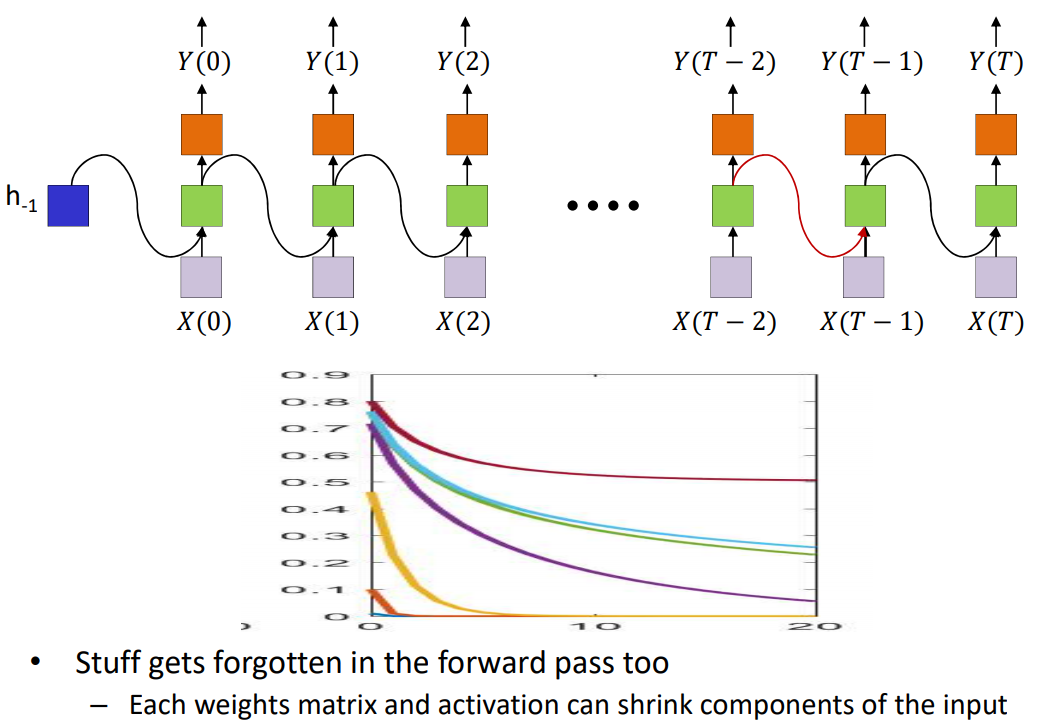
The long-term dependency problem
如图所示,如果pattern1和pattern2之间有太多的内容,RNN将会忘记pattern1。
Exploding/Vanishiing gradients
$$Y = f_{N}(\underline{W_{N-1}f_{N-1}}(\underline{W_{N-2}f_{N-2}}(…\underline{W_0X})))$$
$$\nabla_{f_k}Div=\nabla D·\nabla{f_N}·W_{N-1}\nabla{f_{N-1}·W_{N-2}}…\underline{\nabla{f_{k+1}W_{k}}}$$
- The memory retention of the network depends on the behavior of the underlined terms(网络对于以前信息的记忆主要取决于划线的部分)
- Which in turn depends on the parameters $\color{blue}{W}$ rather than what it is trying to “remember”(主要是依赖于W而不是输入信息)
- Can we have a network that just “remembers” arbitrarily long, to be recalled on demand?
- Not be directly dependent on vagaries(n.奇想,奇特行为; 异想天开; 怪异多变;) of network parameters, but rather on input-based determination of whether it must be remembered
所以针对这些问题是否可以将这些部分替换,怎样使得网路可以记忆任意长度的信息,当需要的时候。
- Not be directly dependent on vagaries(n.奇想,奇特行为; 异想天开; 怪异多变;) of network parameters, but rather on input-based determination of whether it must be remembered
- Replace this with something that doesn’t fade or blow up?
- Network that “retains” useful memory arbitrarily long, to
be recalled on demand?- Input-based determination of whether it must be remembered(基于网络的输入来决定是否记忆)
- Retain memories until a switch based on the input flags them
as ok to forget or remember less
$$Memory(k)\approx C(x)·\sigma_k(x)·\sigma_{k-1}(x)…\sigma_1(x)$$
$$\nabla_{f_k}Div \approx \nabla D\color{red}{C\sigma^{‘}{N}C \sigma^{‘}{N-1}C…\sigma^{‘}_k}$$
