cs231n-assignment3

作业三中总共有五个问题，前两个问题分别是自己实现一个RNN和LSTM来做图像captioning，问题三是对神经网络的几个可视化，问题四是我们经常看到的风格迁移，最后一个问题是生成对抗网络，下面将对每个问题进行详细的阐述。所有作业的实现都已经上传到GitHub。

Q1: Image Captioning with Vanilla RNNs

在Q1和Q2所用到的训练数据集是Microsoft COCO，其中数据进行了预处理，全部的数据特征都是从VGG-16的fc7层中提取的，VGG网络是在ImageNet数据集上预训练好的。通过VGG网络提取的预处理的特征分别存储在train2014_vgg16_fc7.h5和val2014_vgg16_fc7.h5中。为了在速度和处理时间上节省内存，这里使用PCA对提取的特征进行了降维，将VGG-16提取的4096维度降到了512维，存储在train2014_vgg16_fc7_pca.h5和val2014_vgg16_fc7_pca.h5中。为了便于训练每个单词都有一个ID与其对应，这些映射存储在coco2014_vocab.json。下图为训练的数据集。训练中增加了几个特殊的token，在开始和结束的位置分别加了<START>和<END>标签，不常见的单词用<<UNK>来替代，对于长度比较短的在<END>后面用<NULL>来进行补全。

<START> a <UNK> bike learning up against the side of a building <END>	<START> a desk and chair with a computer and a lamp <END>

RNN的实现代码在cs231n/rnn_layers.py中，其中RNN的主要公式如下：

$z=W_xx_t + W_hh_{t-1}+b$ $h_{t} = \tanh(z)$ 作业中会对RNN的前向传播和反向传播分别进行实现，前向传播和反向传播的代码如下:

前向传播

def rnn_step_forward(x, prev_h, Wx, Wh, b):
    """
    Run the forward pass for a single timestep of a vanilla RNN that uses a tanh
    activation function.

    The input data has dimension D, the hidden state has dimension H, and we use
    a minibatch size of N.

    Inputs:
    - x: Input data for this timestep, of shape (N, D).
    - prev_h: Hidden state from previous timestep, of shape (N, H) 
    - Wx: Weight matrix for input-to-hidden connections, of shape (D, H) 
    - Wh: Weight matrix for hidden-to-hidden connections, of shape (H, H) 
    - b: Biases of shape (H,) 

    Returns a tuple of:
    - next_h: Next hidden state, of shape (N, H) 
    - cache: Tuple of values needed for the backward pass. 
    """
    next_h, cache = None, None
    z = np.dot(x, Wx) + np.dot(prev_h, Wh) + b
    next_h = np.tanh(z)
    cache = (x, prev_h, Wx, Wh, b, next_h)
    return next_h, cache

反向传播

def rnn_step_backward(dnext_h, cache):
    """
    Backward pass for a single timestep of a vanilla RNN.

    Inputs:
    - dnext_h: Gradient of loss with respect to next hidden state, of shape (N, H)
    - cache: Cache object from the forward pass

    Returns a tuple of:
    - dx: Gradients of input data, of shape (N, D)
    - dprev_h: Gradients of previous hidden state, of shape (N, H)
    - dWx: Gradients of input-to-hidden weights, of shape (D, H)
    - dWh: Gradients of hidden-to-hidden weights, of shape (H, H)
    - db: Gradients of bias vector, of shape (H,)
    """
    dx, dprev_h, dWx, dWh, db = None, None, None, None, None
    (x, prev_h, Wx, Wh, b, next_h) = cache
    dz = (1 -  next_h**2) * dnext_h
    dx = np.dot(dz, Wx.T)
    dprev_h = np.dot(dz, Wh.T)
    dWx = np.dot(x.T, dz)
    dWh = np.dot(prev_h.T, dz)
    db = np.sum(dz, axis=0) 
    return dx, dprev_h, dWx, dWh, db

以上实现的反向传播和前向传播只是针对于当前时刻的。为了训练需要将时序T加入到RNN的前项传播中，加入时序的前向传播和反向传播如下：

def rnn_forward(x, h0, Wx, Wh, b):
    """
    Run a vanilla RNN forward on an entire sequence of data. We assume an input
    sequence composed of T vectors, each of dimension D. The RNN uses a hidden
    size of H, and we work over a minibatch containing N sequences. After running
    the RNN forward, we return the hidden states for all timesteps.

    Inputs:
    - x: Input data for the entire timeseries, of shape (N, T, D).
    - h0: Initial hidden state, of shape (N, H)
    - Wx: Weight matrix for input-to-hidden connections, of shape (D, H)
    - Wh: Weight matrix for hidden-to-hidden connections, of shape (H, H)
    - b: Biases of shape (H,)

    Returns a tuple of:
    - h: Hidden states for the entire timeseries, of shape (N, T, H).
    - cache: Values needed in the backward pass
    """
    h, cache = None, None
    h = []
    cache = []
    h.append(h0)
    N, T, _ = x.shape
    for t in range(T):
        x_t = x[:,t,:]
        prev_h = h[t]
        next_h, cache_t = rnn_step_forward(x_t, prev_h, Wx, Wh, b)
        h.append(next_h)
        cache.append(cache_t)
    h = np.hstack(h[1:]).reshape(N, T, -1)
    return h, cache


def rnn_backward(dh, cache):
    """
    Compute the backward pass for a vanilla RNN over an entire sequence of data.

    Inputs:
    - dh: Upstream gradients of all hidden states, of shape (N, T, H). 下一层网络的梯度信息
    
    NOTE: 'dh' contains the upstream gradients produced by the 
    individual loss functions at each timestep, *not* the gradients
    being passed between timesteps (which you'll have to compute yourself
    by calling rnn_step_backward in a loop).

    Returns a tuple of:
    - dx: Gradient of inputs, of shape (N, T, D)
    - dh0: Gradient of initial hidden state, of shape (N, H)
    - dWx: Gradient of input-to-hidden weights, of shape (D, H)
    - dWh: Gradient of hidden-to-hidden weights, of shape (H, H)
    - db: Gradient of biases, of shape (H,)
    """
    dx, dh0, dWx, dWh, db = None, None, None, None, None
    N, T, H = dh.shape
    dx = []
    dprev_h = 0
    dWx = 0
    dWh = 0
    db = 0
    for t in range(T-1, -1, -1):
        cache_cur = cache[t]
        dnext_h = dprev_h + dh[:, t, :]
        dcurx, dprev_h, dWx_, dWh_, db_ = rnn_step_backward(dnext_h, cache_cur)
        dWx += dWx_
        dWh += dWh_
        db += db_
        dx.append(dcurx)
    dx.reverse()
    dx = np.hstack(dx).reshape(N, T, -1)
    dh0 = dprev_h
    return dx, dh0, dWx, dWh, db

这里需要注意的主要是RNN的反向传播的实现，在反向传播中有下一层传回来的时序的梯度这里是dh，可以看到它的shape大小为(N, T, H)。在前向传播的过程中隐层的状态信息分两条线路，一部分传到下个时刻，一部分传到下一层网络，如图所示：

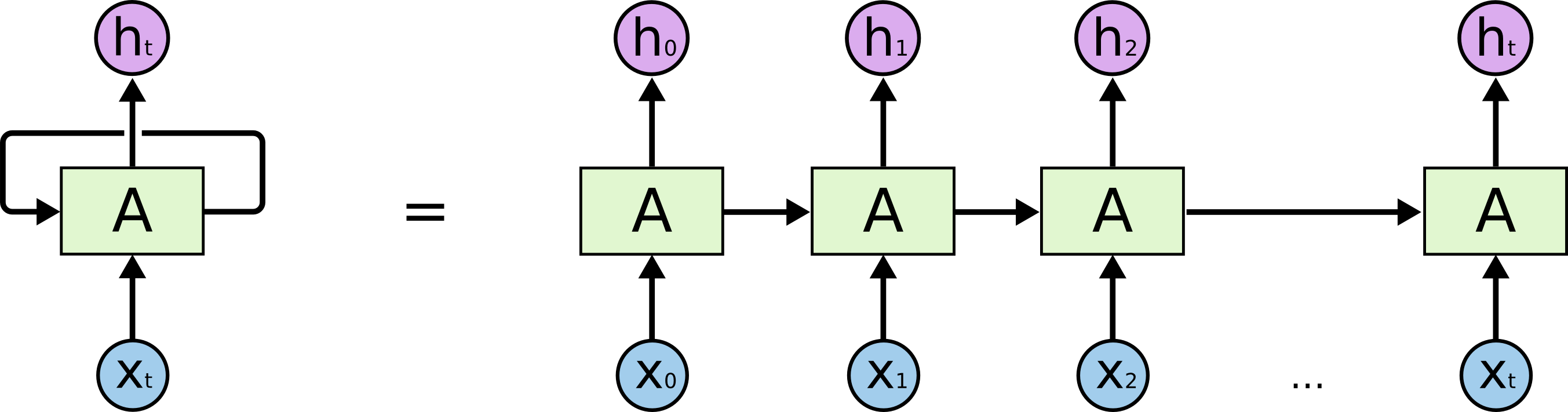对于h1来说分两部分，分别传到下层和T2时刻的隐藏层输入，所以在反向传播的时候h1有两部分的梯度一部分是下一层的，实现的时候为dh[:, t, :]，一部分为下一个时刻的为dprev_h。同时对于T时刻的状态，dprev_h=0。

Q2: Image Captioning with LSTMs

LSTM训练所用到的数据集同RNN相同，LSTM同RNN相同，在每个时刻接受一个输入和上一层的隐藏层的状态，LSTM也保持着之前的状态在cell state $c_{t-1}\in\mathbb{R}^H$ 。 在LSTM中可以学习的参数有两个一个是input-to-hidden 的权重 $W_x\in\mathbb{R}^{4H\times D}$, 另一个是 hidden-to-hidden 的权重 $W_h\in\mathbb{R}^{4H\times H}$ 还有一个 bias vector $b\in\mathbb{R}^{4H}$。这边具体的描述直接copy的代码页的描述不做翻译了。

At each timestep we first compute an activation vector $a\in\mathbb{R}^{4H}$ as $a=W_xx_t + W_hh_{t-1}+b$. We then divide this into four vectors $a_i,a_f,a_o,a_g\in\mathbb{R}^H$ where $a_i$ consists of the first $H$ elements of $a$, $a_f$ is the next $H$ elements of $a$, etc. We then compute the input gate $g\in\mathbb{R}^H$, forget gate $f\in\mathbb{R}^H$, output gate $o\in\mathbb{R}^H$ and block input $g\in\mathbb{R}^H$ as
$$
i = \sigma(a_i) \hspace{4pc} f = \sigma(a_f) \hspace{4pc} o = \sigma(a_o) \hspace{4pc} g = \tanh(a_g)
$$
where $\sigma$ is the sigmoid function and $\tanh$ is the hyperbolic tangent, both applied elementwise.
Finally we compute the next cell state $c_t$ and next hidden state $h_t$ as
$$
c_{t} = f\odot c_{t-1} + i\odot g \hspace{4pc}
h_t = o\odot\tanh(c_t)
$$
where $\odot$ is the elementwise product of vectors.
In the rest of the notebook we will implement the LSTM update rule and apply it to the image captioning task.
In the code, we assume that data is stored in batches so that $X_t \in \mathbb{R}^{N\times D}$, and will work with transposed versions of the parameters: $W_x \in \mathbb{R}^{D \times 4H}$, $W_h \in \mathbb{R}^{H\times 4H}$ so that activations $A \in \mathbb{R}^{N\times 4H}$ can be computed efficiently as $A = X_t W_x + H_{t-1} W_h$

def lstm_step_forward(x, prev_h, prev_c, Wx, Wh, b):
    """
    Forward pass for a single timestep of an LSTM.

    The input data has dimension D, the hidden state has dimension H, and we use
    a minibatch size of N.

    Note that a sigmoid() function has already been provided for you in this file.

    Inputs:
    - x: Input data, of shape (N, D)
    - prev_h: Previous hidden state, of shape (N, H)
    - prev_c: previous cell state, of shape (N, H)
    - Wx: Input-to-hidden weights, of shape (D, 4H)
    - Wh: Hidden-to-hidden weights, of shape (H, 4H)
    - b: Biases, of shape (4H,)

    Returns a tuple of:
    - next_h: Next hidden state, of shape (N, H)
    - next_c: Next cell state, of shape (N, H)
    - cache: Tuple of values needed for backward pass.
    """
    next_h, next_c, cache = None, None, None
    a = np.dot(x, Wx) + np.dot(prev_h, Wh) + b
    a_i, a_f, a_o, a_g = np.hsplit(a, 4)
    i = sigmoid(a_i)
    f = sigmoid(a_f)
    o = sigmoid(a_o)
    g = np.tanh(a_g)
    next_c = f * prev_c + i * g
    next_h = o * np.tanh(next_c)
    cache = (next_h, o, f, prev_c, i, g, x, Wx, prev_h, Wh)
    return next_h, next_c, cache


def lstm_step_backward(dnext_h, dnext_c, cache):
    """
    Backward pass for a single timestep of an LSTM.

    Inputs:
    - dnext_h: Gradients of next hidden state, of shape (N, H)
    - dnext_c: Gradients of next cell state, of shape (N, H)
    - cache: Values from the forward pass

    Returns a tuple of:
    - dx: Gradient of input data, of shape (N, D)
    - dprev_h: Gradient of previous hidden state, of shape (N, H)
    - dprev_c: Gradient of previous cell state, of shape (N, H)
    - dWx: Gradient of input-to-hidden weights, of shape (D, 4H)
    - dWh: Gradient of hidden-to-hidden weights, of shape (H, 4H)
    - db: Gradient of biases, of shape (4H,)
    """
    dx, dprev_h, dprev_c, dWx, dWh, db = None, None, None, None, None, None
    (next_h, o, f, prev_c, i, g, x, Wx, prev_h, Wh) = cache
    dnext_c += dnext_h * o * (1 - (next_h / o)**2)
    dprev_c = dnext_c * f
    df = dnext_c * prev_c
    do = dnext_h * next_h / o
    di = dnext_c * g
    dg = dnext_c * i
    da_i = di * i * (1-i)
    da_f = df * f * (1-f)
    da_o = do * o * (1-o)
    da_g = dg * (1-g**2)
    da = np.concatenate((da_i, da_f, da_o, da_g), axis=1)
    db = np.sum(da, axis=0)
    dx = np.dot(da, Wx.T)
    dWx = np.dot(x.T, da)
    dprev_h = np.dot(da, Wh.T)
    dWh = np.dot(prev_h.T, da)
    return dx, dprev_h, dprev_c, dWx, dWh, db


def lstm_forward(x, h0, Wx, Wh, b):
    """
    Forward pass for an LSTM over an entire sequence of data. We assume an input
    sequence composed of T vectors, each of dimension D. The LSTM uses a hidden
    size of H, and we work over a minibatch containing N sequences. After running
    the LSTM forward, we return the hidden states for all timesteps.

    Note that the initial cell state is passed as input, but the initial cell
    state is set to zero. Also note that the cell state is not returned; it is
    an internal variable to the LSTM and is not accessed from outside.

    Inputs:
    - x: Input data of shape (N, T, D)
    - h0: Initial hidden state of shape (N, H)
    - Wx: Weights for input-to-hidden connections, of shape (D, 4H)
    - Wh: Weights for hidden-to-hidden connections, of shape (H, 4H)
    - b: Biases of shape (4H,)

    Returns a tuple of:
    - h: Hidden states for all timesteps of all sequences, of shape (N, T, H)
    - cache: Values needed for the backward pass.
    """
    h, cache = None, None
    N, T, D = x.shape
    prev_h = h0
    prev_c = 0
    cache = []
    h = []
    for t in range(T):
        x_t = x[:, t, :]
        next_h, next_c, cache_ = lstm_step_forward(x_t, prev_h, prev_c, Wx, Wh, b)
        prev_h = next_h
        prev_c = next_c
        cache.append(cache_)
        h.append(next_h)
    
    h = np.hstack(h).reshape(N, T, -1)
    return h, cache


def lstm_backward(dh, cache):
    """
    Backward pass for an LSTM over an entire sequence of data.]

    Inputs:
    - dh: Upstream gradients of hidden states, of shape (N, T, H)
    - cache: Values from the forward pass

    Returns a tuple of:
    - dx: Gradient of input data of shape (N, T, D)
    - dh0: Gradient of initial hidden state of shape (N, H)
    - dWx: Gradient of input-to-hidden weight matrix of shape (D, 4H)
    - dWh: Gradient of hidden-to-hidden weight matrix of shape (H, 4H)
    - db: Gradient of biases, of shape (4H,)
    """
    dx, dh0, dWx, dWh, db = None, None, None, None, None
    (N, T, H) = dh.shape
    dprev_h = 0
    dprev_c = 0
    dx = []
    dWx = 0; dWh = 0; db = 0
    for t in reversed(range(T)):
        cache_ = cache[t]
        dnext_h = dh[:, t, :] + dprev_h
        dnext_c = dprev_c
        dx_, dprev_h, dprev_c, dWx_, dWh_, db_ = lstm_step_backward(dnext_h, dnext_c, cache_)
        dx.append(dx_)
        dWx += dWx_
        dWh += dWh_
        db += db_
        
    dh0 = dprev_h
    dx = np.hstack(list(reversed(dx))).reshape(N, T, -1)
    return dx, dh0, dWx, dWh, db

Q3: Network Visualization: Saliency maps, Class Visualization, and Fooling Images

Q4: Style Transfer

Q5: Generative Adversarial Networks